Двойные интегралы и пределы интегрирования

Двойной интеграл функции $f\left(x,y\right)$ по области интегрирования $\Omega$ на плоскости (за определением которого я отсылаю к лекциям), может быть представлен в виде повторного интеграла, то есть в виде определённого интеграла от определённого интеграла от функции $f\left(x,y\right)$: \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\int\limits _{a}^{b}\left[\int\limits _{\alpha(x)}^{\beta(x)}f\left(x,y\right)dy\right]dx=\int\limits _{a}^{b}dx\int\limits _{\alpha(x)}^{\beta(x)}f\left(x,y\right)dy. \]

Квадратные скобки выше добавлены для понятности структуры выражения и обычно не ставятся. Пределы интегрирования $a$ и $b$ для внешнего из этих двух интегралов – это наименьшее и наибольшее значение переменной интегрирования (в данном случае $x$) на всей области интегрирования. Пределы интегрирования $\alpha(x)$ и $\beta(x)$ для внутреннего интеграла – это наименьшее и наибольшее значение переменной интегрирования $y$ при данном $x$. Иначе говоря, это функции, графики которых являются нижней и верхней границами области $\Omega$.

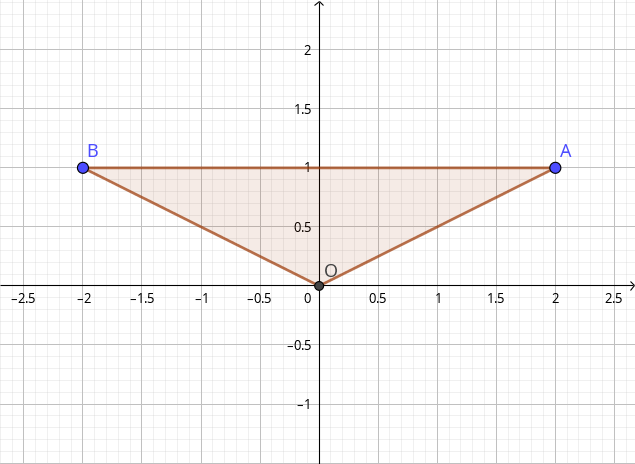
Например, возьмём № 3917 из Демидовича, где $\Omega$ – треугольник с вершинами $O\left(0,0\right)$, $A\left(2,1\right)$, $B\left(-2,1\right)$.

Значение $x$ для точек этого треугольника лежит от $a=-2$ до $b=2$. Сверху треугольник ограничен отрезком прямой $y=1$, а снизу – графиком $y=\frac{\left|x\right|}{2}$; поэтому $\alpha(x)=\frac{\left|x\right|}{2}$, а $\beta(x)=1$: \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\int\limits _{-2}^{2}dx\int\limits _{|x|/2}^{1}f\left(x,y\right)dy. \]

Можно, однако, и в обратном порядке расставить интегралы: сначала по у, потом по х. \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\int\limits _{c}^{d}\left[\int\limits _{\varphi(y)}^{\psi(y)}f\left(x,y\right)dx\right]dy=\int\limits _{c}^{d}dy\int\limits _{\varphi(y)}^{\psi(y)}f\left(x,y\right)dx. \] Теперь $c$ и $d$ для внешнего интеграла – это наименьшее и наибольшее значение переменной интегрирования $y$ на всей области интегрирования, а $\varphi(x)$ и $\psi(x)$ для внутреннего интеграла – это функции, графики которых $y=\varphi(x)$ и $y=\psi(x)$ являются левой и правой границами области $\Omega$ соответственно.

Для интеграла из № 3917 низшая точка треугольника имеет $y=0$, а высшие – $y=1$. При этом левая граница (отрезок, соединяющий точки $B$ и $O$) задаётся уравнением $y=-\frac{x}{2}$, а правая – $y=\frac{x}{2}$. Тогда \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\int\limits _{0}^{1}dy\int\limits _{-x/2}^{x/2}f\left(x,y\right)dx. \]

Задание: № 3916, 3919, 3920.

Если области $\Omega_{1}$ и $\Omega_{2}$ такие, что их объединение даёт всю $\Omega$, а их пересечение имеет нулевую площадь, то говорят, что $\Omega_{1}$ и $\Omega_{2}$ образуют разбиение $\Omega$. Интеграл по области $\Omega$ равен сумме интегралов по элементам разбиения: \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\iint\limits _{\Omega_{1}}f\left(x,y\right)dxdy+\iint\limits _{\Omega_{2}}f\left(x,y\right)dxdy. \] В некоторых номерах можно воспользоваться этим, например в № 3918.

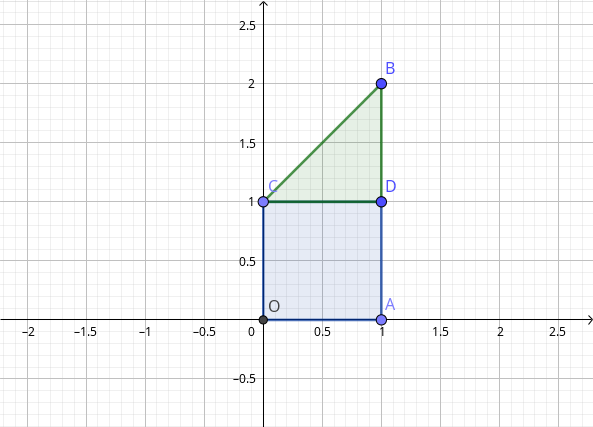
При вынесении наружу интеграла по $x$ всё просто: \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\int\limits _{0}^{1}dx\int\limits _{0}^{x+1}f\left(x,y\right)dy. \] Но если делать наоборот, становится сложно описать одной функцией левую границу трапеции. Поэтому можно добавить точку $D\left(1,1\right)$, и всю трапецию разложить на квадрат $OADC$ ($0\leqslant y\leqslant1$, $0\leqslant x\leqslant1$) и треугольник $CDB$, чья левая граница есть отрезок прямой $y=x+1$ или $x=y-1$. Так как на эти фигуры разбивается исходная трапеция, интеграл по трапеции равен сумме интегралов по квадрату и треугольнику:

\[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\iint\limits _{\Box}f\left(x,y\right)dxdy+\iint\limits _{\bigtriangleup}f\left(x,y\right)dxdy= \] \[ =\int\limits _{0}^{1}dy\int\limits _{0}^{1}f\left(x,y\right)dx+\int\limits _{1}^{2}dy\int\limits _{y-1}^{1}f\left(x,y\right)dx. \]

Задание: № 3921.

Бывает, что двойной интеграл уже выражен в виде двух вложенных, но нас не устраивает порядок переменных, по которым предполагается интегрировать (а от него зависит многое, иногда и сама возможность взять интеграл). Тогда порядок интегрирования надо поменять. При этом сначала строится область интегрирования по пределам в интегралах, потом – по этой области определяются пределы, но уже для интегралов в обратном порядке.

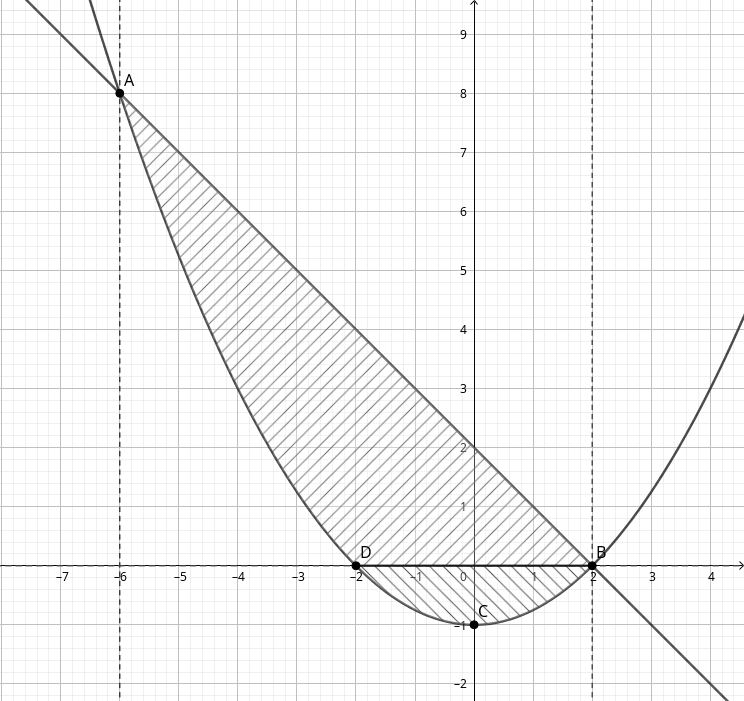
Пример: № 3925 \[ \int\limits _{-6}^{2}dx\int\limits _{\left(x^{2}/4\right)-1}^{2-x}f\left(x,y\right)dy. \] Область интегрирования тут ограничена линиями $x=-6$, $x=2$, $y=\frac{x^{2}}{4}-1$, $y=2-x$.

Начертив все линии, получим фигуру $ABC$ (заметим, что парабола и наклонная прямая имеют точки пересечения с абсциссами как раз -6 и 2). Как и в предыдущем номере, разобьём область интегрирования на две: $ABD$ и $BCD$; затем представим интеграл в виде суммы интегралов по ним.

Фигура $BCD$ по оси $y$ простирается от $y=-1$ до $y=0$, слева и справа ограничиваясь параболой $y=\frac{x^{2}}{4}-1$. Решая это уравнение, получим $x=\pm2\sqrt{y+1}$, где решение $x=-2\sqrt{y+1}$ описывает левую границу, а $x=2\sqrt{y+1}$ – правую. Итак, \[ \iint\limits _{BCD}f\left(x,y\right)dxdy=\int\limits _{-1}^{0}dy\int\limits _{-2\sqrt{y+1}}^{2\sqrt{y+1}}f\left(x,y\right)dx. \] Фигура $ABD$ по оси $y$ простирается от $y=0$ до $y=8$, слева ограничиваясь параболой $y=\frac{x^{2}}{4}-1$, а справа – прямой $y=2-x$. Решая уравнение параболы, выберем решение $x=-2\sqrt{y+1}$, так как $x$ на левой границе отрицателен. Справа же $x=2-x$: \[ \iint\limits _{ABD}f\left(x,y\right)dxdy=\int\limits _{0}^{8}dy\int\limits _{-2\sqrt{y+1}}^{2-x}f\left(x,y\right)dx. \] Общий же интеграл \[ \int\limits _{-6}^{2}dx\int\limits _{\left(x^{2}/4\right)-1}^{2-x}f\left(x,y\right)dy=\iint\limits _{BCD}f\left(x,y\right)dxdy+\iint\limits _{ABD}f\left(x,y\right)dxdy= \] \[ =\int\limits _{-1}^{0}dy\int\limits _{-2\sqrt{y+1}}^{2\sqrt{y+1}}f\left(x,y\right)dx+\int\limits _{0}^{8}dy\int\limits _{-2\sqrt{y+1}}^{2-x}f\left(x,y\right)dx. \]

Свойства двойных интегралов и замена переменных

Помимо упомянутого выше свойства аддитивности \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\iint\limits _{\Omega_{1}}f\left(x,y\right)dxdy+\iint\limits _{\Omega_{2}}f\left(x,y\right)dxdy, \] двойные интегралы обладают свойством линейности: \[ \iint\limits _{\Omega}\left[\alpha f\left(x,y\right)+\beta g\left(x,y\right)\right]dxdy=\alpha\iint\limits _{\Omega}f\left(x,y\right)dxdy+\beta\iint\limits _{\Omega}g\left(x,y\right)dxdy \] Также в них можно заменять переменные. Выражается эта возможность формулой такой: \[ \iint\limits _{\Omega}f\left(x,y\right)dxdy=\iint\limits _{\Sigma}f\left(x(u,v),y(u,v)\right)\left|J\right|dudv, \] где $u$ и $v$ – новые переменные, связанные со старыми уравнениями перехода типа \[ \left\{ \begin{array}{c} x=x\left(u,v\right),\\ y=y\left(u,v\right). \end{array}\right. \] $J$ – определитель матрицы, называемый якобианом \[ J=\left|\begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array}\right|, \] а область $\Sigma$ – область, которую принимают новые переменные.

В частности, вместо декартовых часто используются так называемые полярные координаты, рассматривавшиеся ещё на первом курсе в связи с тригонометрической формой комплексного числа. Это координаты $r$ и $\varphi$, которые связаны с $x$ и $y$ так: \[ \left\{ \begin{array}{c} x=r\cos\varphi,\\ y=r\sin\varphi. \end{array}\right. \] Якобиан перехода от декартовых координат к полярным вычислим ниже: \[ J=\left|\begin{array}{cc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} \end{array}\right|=\left|\begin{array}{cc} \cos\varphi & -r\sin\varphi\\ \sin\varphi & r\cos\varphi \end{array}\right|=r\left(\cos^{2}\varphi+\sin^{2}\varphi\right)=r. \]

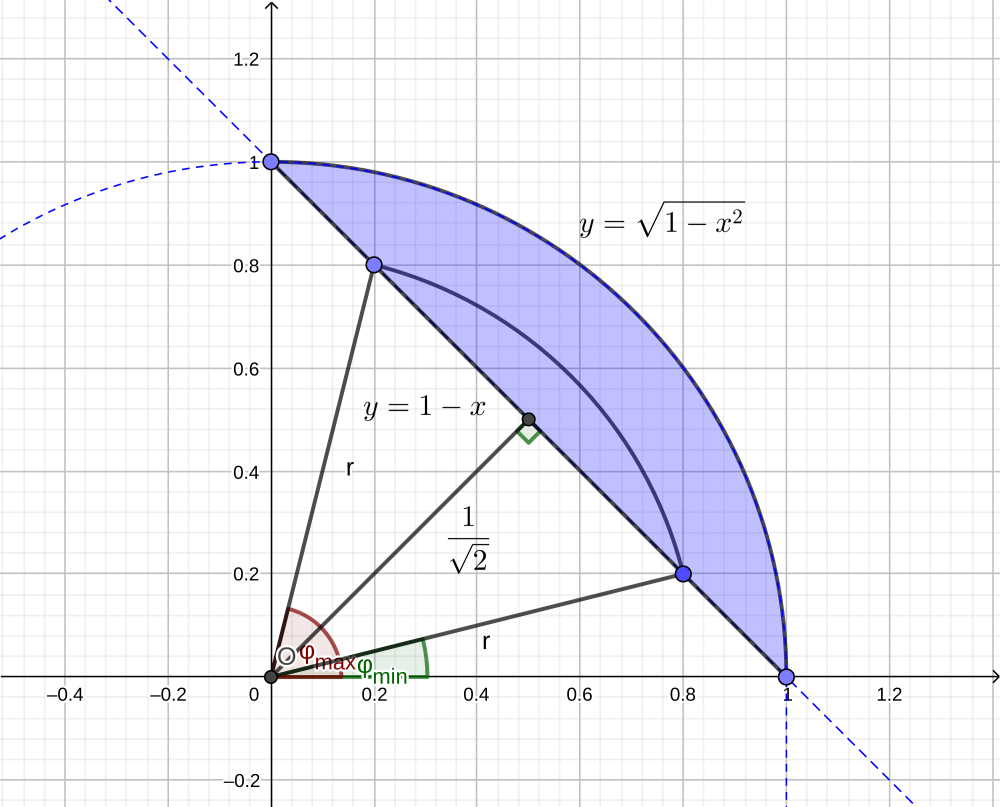
Пример: №3944 Перейти к полярным координатам и расставить пределы интегрирования в том и в другом порядке в интеграле

\[ \intop_{0}^{1}dx\intop_{1-x}^{\sqrt{1-x^{2}}}dyf\left(x,y\right) \]

Якобиан перехода вычислен выше и равен $r$.

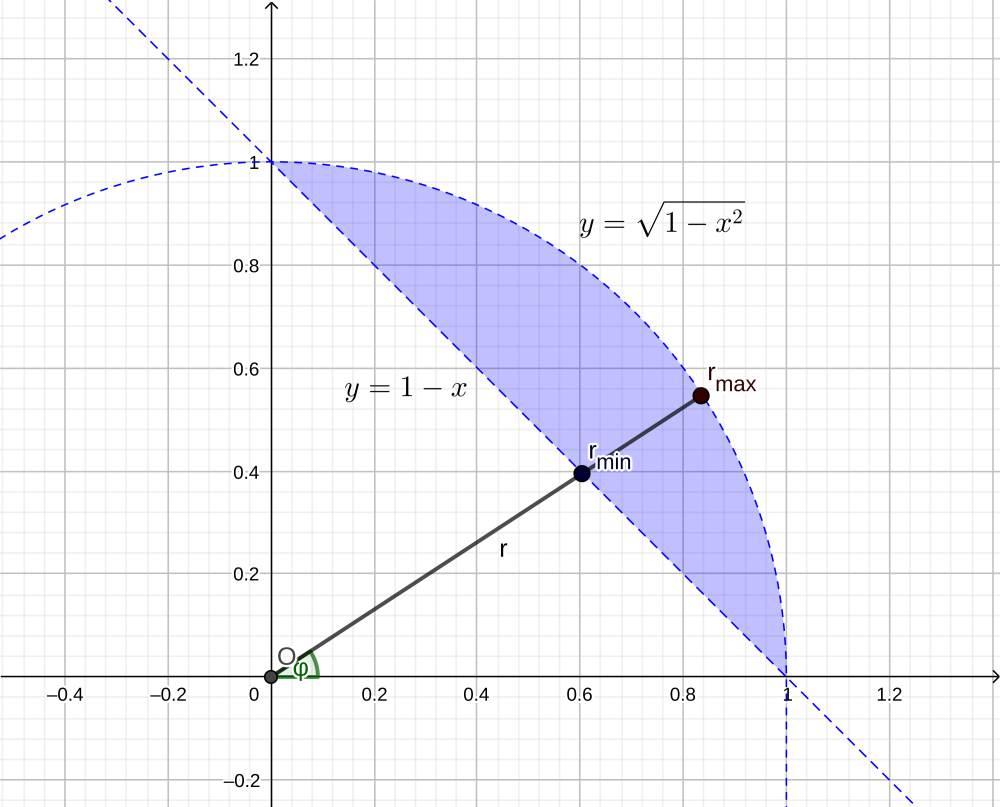
Вначале поставим снаружи интеграл по $d\varphi$: \[ \intop_{0}^{1}dx\intop_{1-x}^{\sqrt{1-x^{2}}}dyf\left(x,y\right)=\intop d\varphi\intop drf\left(x,y\right)r. \] Осталось в последнем интеграле расставить пределы интегрирования. Для координаты $\varphi$ для этого нужно искать наименьшее и наибольшее значения на всей фигуре, которые она примет в точках $\left(1;0\right)$, где $\varphi=0$, и $\left(0;1\right)$, где $\varphi=\frac{\pi}{2}$.

Координата $r$, так как имеет смысл расстояния от начала координат, принимает наибольшие значения на самых дальних точках, т.е. точках дуги единичной окружности, где $r=1$. Наименьшие же значения она принимает в точках хорды, где \[ y=1-x, \] причём для каждого $\varphi$ это значение своё: \[ r\sin\varphi=1-r\cos\varphi, \] \[ r\left(\sin\varphi+\cos\varphi\right)=1, \] \[ r=\frac{1}{\sin\varphi+\cos\varphi}. \] Итак, \[ \intop_{0}^{1}dx\intop_{1-x}^{\sqrt{1-x^{2}}}dyf\left(x,y\right)=\intop_{0}^{\frac{\pi}{2}}d\varphi\intop_{\frac{1}{\sin\varphi+\cos\varphi}}^{1}drf\left(x,y\right)r. \]

Если же теперь снаружи поставить интеграл по $dr$, то придётся искать наименьшее и наибольшее значения $r$ на всей области интегрирования. Наибольшее, как мы уже знаем, равно 1, а наименьшее достигается в точке, в которую падает перпендикуляр к хорде, ограничивающей область интегрирования снизу (рис. 5). Нетрудно видеть, что оно равно $\frac{1}{\sqrt{2}}$.

Множество точек с одинаковым $r$ образует дугу радиуса $r$, которая, проходя через нашу область интегрирования, пересекает хорду $y=1-x$ в двух местах; в левой нижней из этих точек достигается наименьшее значение $\varphi$ при данном $r$, в правой верхней – наибольшее. Находятся они, как и в предыдущем случае, из уравнения хорды в полярных координатах, но теперь мы решаем его относительно $\varphi$: \[ r\left(\sin\varphi+\cos\varphi\right)=1, \] \[ \sin\varphi+\cos\varphi=\cos\left(\frac{\pi}{2}-\varphi\right)+\cos\varphi=2\cos\frac{\pi}{4}\cos\left(\frac{\pi}{4}-\varphi\right)=\sqrt{2}\cos\left(\varphi-\frac{\pi}{4}\right), \] \[ \sqrt{2}\cos\left(\varphi-\frac{\pi}{4}\right)=\frac{1}{r}, \] \[ \varphi-\frac{\pi}{4}=\pm\arccos\frac{1}{\sqrt{2}r}, \] \[ \varphi=\frac{\pi}{4}\pm\arccos\frac{1}{\sqrt{2}r}, \] \[ \varphi_{min}=\frac{\pi}{4}-\arccos\frac{1}{\sqrt{2}r},\qquad\varphi_{max}=\frac{\pi}{4}+\arccos\frac{1}{\sqrt{2}r}; \] тогда \[ \intop_{0}^{1}dx\intop_{1-x}^{\sqrt{1-x^{2}}}dyf\left(x,y\right)=\intop_{1/\sqrt{2}}^{1}dr\intop_{\frac{\pi}{4}-\arccos\frac{1}{\sqrt{2}r}}^{\frac{\pi}{4}+\arccos\frac{1}{\sqrt{2}r}}d\varphi f\left(x,y\right)r. \]

Задание: № 3943, 3945.