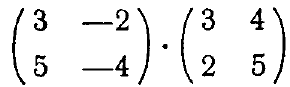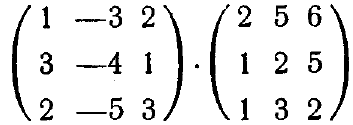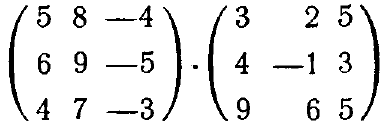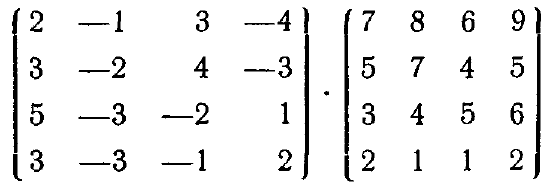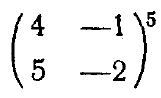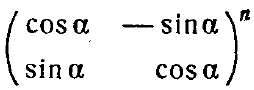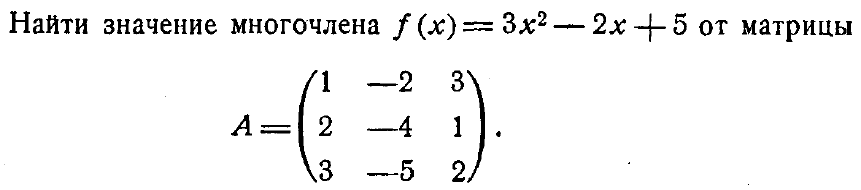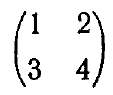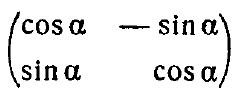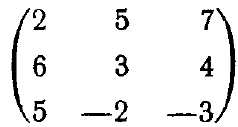Матрица – это множество чисел, каждое из которых имеет два номера (их ещё называют индексами): $a_{ik}$. Первый номер (в данном примере $i$) называется номером строки, второй – номером столбца. Можно считать матрицу таблицей чисел. \[ \begin{array}{c} \\i\\ \\\\\\\\\end{array} \stackrel{ \begin{array}{cccccc} k & & & & \end{array} }{\left(\begin{array}{cccccccc} a_{11} & \dots & & & & & \dots & a_{1m}\\ \vdots & & a_{ik} & & & & & \vdots\\ \\\\\vdots & & & & & & & \vdots\\ a_{n1} & \dots & & & & & \dots & a_{nm} \end{array}\right)} \]
Матрицы обычно обозначаются заглавными латинскими буквами. Числа, входящие в матрицу, называются её элементами. Количество строк вместе с количеством столбцов называется размером матрицы.
Вот, например, матрица размером 2х3: \[ \left(\begin{array}{ccc} 1 & 2 & 3\\ 4 & 5 & 6 \end{array}\right), \] а вот размером 3х2: \[ \left(\begin{array}{cr} 0 & 1\\ 2 & 0\\ -1 & -2 \end{array}\right). \] Матрицы, у которых количество строк и столбцов одинаково, называются квадратными. Элементы, у которых индексы равны, лежат на главной диагонали.
Действия с матрицами
Умножение матрицы на число
\[ \alpha A=C \] При этом каждый элемент исходной матрицы умножается на это число: \[ \alpha a_{ij}=c_{ij} \] Пример \[ 2\left(\begin{array}{ccc} 1 & 2 & 1\\ 3 & 1 & 3\\ 1 & 2 & 1 \end{array}\right)=\left(\begin{array}{ccc} 2 & 4 & 2\\ 6 & 2 & 6\\ 2 & 4 & 2 \end{array}\right) \]
Сложение матриц
\[ A+B=C \] Каждый элемент первого слагаемого складывается с соответствующим (т.е. стоящим на том же месте) элементом второго слагаемого : \[ a_{ij}+b_{ij}=c_{ij} \] Пример: \[ \left(\begin{array}{ccc} 1 & \boxed{2} & 1\\ 3 & 1 & 3\\ 1 & 2 & 1 \end{array}\right)+\left(\begin{array}{ccc} 1 & \boxed{3} & 1\\ 2 & 1 & 2\\ 1 & 3 & 1 \end{array}\right)=\left(\begin{array}{ccc} 2 & \boxed{5} & 2\\ 5 & 2 & 5\\ 2 & 5 & 2 \end{array}\right). \] Можно заметить, что складывать между собой можно не любые матрицы, а только имеющие одинаковые размеры. Матрицы в сумме очевидно можно переставлять, а ещё среди матриц одного размера всегда есть нулевая матрица, прибавление которой не меняет исходную. Она состоит из нулей: \[ \left(\begin{array}{ccc} 1 & 2 & 1\\ 3 & 1 & 3\\ 1 & 2 & 1 \end{array}\right)+\left(\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right)=\left(\begin{array}{ccc} 1 & 2 & 1\\ 3 & 1 & 3\\ 1 & 2 & 1 \end{array}\right). \]
Умножение матриц
\[ A\cdot B=C \] Это более сложная операция. Элемент произведения вычисляется по формуле \[ \sum_{k=1}^{n}a_{ik}b_{kj}=c_{ij}, \] иначе, чтобы получить элемент произведения $c_{ij}$, надо перемножить элементы строки $i$ из первого множителя и столбца $j$ из второго множителя, а потом сложить эти произведения.
Пример: \[ \left(\begin{array}{ccc} 1 & 2 & 1\\ 3 & 1 & 3\\ 1 & 2 & 1 \end{array}\right)\cdot\left(\begin{array}{ccc} 1 & 3 & 1\\ 2 & 1 & 2\\ 1 & 3 & 1 \end{array}\right)=\left(\begin{array}{ccc} 6 & 8 & 6\\ 8 & 19 & 8\\ 6 & 8 & 6 \end{array}\right) \] Получим отдельно$c_{11}$: \[ \left(\begin{array}{c} \boxed{\begin{array}{ccc} 1 & 2 & 1\end{array}}\\ \begin{array}{ccc} 3 & 1 & 3\end{array}\\ \begin{array}{ccc} 1 & 2 & 1\end{array} \end{array}\right)\cdot\left(\begin{array}{ccc} \boxed{\begin{array}{c} 1\\ 2\\ 1 \end{array}} & \begin{array}{c} 3\\ 1\\ 3 \end{array} & \begin{array}{c} 1\\ 2\\ 1 \end{array}\end{array}\right)=\left(\begin{array}{ccc} \boxed{6} & 8 & 6\\ 8 & 19 & 8\\ 6 & 8 & 6 \end{array}\right) \] \[ 1\cdot1+2\cdot2+1\cdot1=6 \] Теперь $c_{12}$: \[ \left(\begin{array}{c} \boxed{\begin{array}{ccc} 1 & 2 & 1\end{array}}\\ \begin{array}{ccc} 3 & 1 & 3\end{array}\\ \begin{array}{ccc} 1 & 2 & 1\end{array} \end{array}\right)\cdot\left(\begin{array}{ccc} \begin{array}{c} 1\\ 2\\ 1 \end{array} & \boxed{\begin{array}{c} 3\\ 1\\ 3 \end{array}} & \begin{array}{c} 1\\ 2\\ 1 \end{array}\end{array}\right)=\left(\begin{array}{ccc} 6 & \boxed{8} & 6\\ 8 & 19 & 8\\ 6 & 8 & 6 \end{array}\right) \] \[ 1\cdot3+2\cdot1+1\cdot3=8 \] $c_{13}$ \[ \left(\begin{array}{c} \boxed{\begin{array}{ccc} 1 & 2 & 1\end{array}}\\ \begin{array}{ccc} 3 & 1 & 3\end{array}\\ \begin{array}{ccc} 1 & 2 & 1\end{array} \end{array}\right)\cdot\left(\begin{array}{ccc} \begin{array}{c} 1\\ 2\\ 1 \end{array} & \begin{array}{c} 3\\ 1\\ 3 \end{array} & \boxed{\begin{array}{c} 1\\ 2\\ 1 \end{array}}\end{array}\right)=\left(\begin{array}{ccc} 6 & 8 & \boxed{6}\\ 8 & 19 & 8\\ 6 & 8 & 6 \end{array}\right) \] \[ 1\cdot1+2\cdot2+1\cdot1=6 \] Теперь элементы второй строки. $c_{21}$: \[ \left(\begin{array}{c} \begin{array}{ccc} 1 & 2 & 1\end{array}\\ \boxed{\begin{array}{ccc} 3 & 1 & 3\end{array}}\\ \begin{array}{ccc} 1 & 2 & 1\end{array} \end{array}\right)\cdot\left(\begin{array}{ccc} \boxed{\begin{array}{c} 1\\ 2\\ 1 \end{array}} & \begin{array}{c} 3\\ 1\\ 3 \end{array} & \begin{array}{c} 1\\ 2\\ 1 \end{array}\end{array}\right)=\left(\begin{array}{ccc} 6 & 8 & 6\\ \boxed{8} & 19 & 8\\ 6 & 8 & 6 \end{array}\right) \] \[ 3\cdot1+1\cdot2+3\cdot1=8 \] $c_{22}$ \[ \left(\begin{array}{c} \begin{array}{ccc} 1 & 2 & 1\end{array}\\ \boxed{\begin{array}{ccc} 3 & 1 & 3\end{array}}\\ \begin{array}{ccc} 1 & 2 & 1\end{array} \end{array}\right)\cdot\left(\begin{array}{ccc} \begin{array}{c} 1\\ 2\\ 1 \end{array} & \boxed{\begin{array}{c} 3\\ 1\\ 3 \end{array}} & \begin{array}{c} 1\\ 2\\ 1 \end{array}\end{array}\right)=\left(\begin{array}{ccc} 6 & 8 & 6\\ 8 & \boxed{19} & 8\\ 6 & 8 & 6 \end{array}\right) \] \[ 3\cdot3+1\cdot1+3\cdot3=9+1+9=19 \] $c_{23}$ \[ \left(\begin{array}{c} \begin{array}{ccc} 1 & 2 & 1\end{array}\\ \boxed{\begin{array}{ccc} 3 & 1 & 3\end{array}}\\ \begin{array}{ccc} 1 & 2 & 1\end{array} \end{array}\right)\cdot\left(\begin{array}{ccc} \begin{array}{c} 1\\ 2\\ 1 \end{array} & \begin{array}{c} 3\\ 1\\ 3 \end{array} & \boxed{\begin{array}{c} 1\\ 2\\ 1 \end{array}}\end{array}\right)=\left(\begin{array}{ccc} 6 & 8 & 6\\ 8 & 19 & \boxed{8}\\ 6 & 8 & 6 \end{array}\right) \] \[ 3\cdot1+1\cdot2+3\cdot1=8 \] и так далее.
Из определения следует, что на все элементы строки первого множителя должно хватить элементов столбца из второго. Поэтому можно умножать не все матрицы, а только те, у которых соблюдается вышеописанный паритет; иными словами, число столбцов первой матрицы должно равняться числу строк второй. Автоматически можно умножать квадратные матрицы одинакового размера.
Среди квадратных матриц существуют т.н. единичные $E_{n}$, умножение на которые ничего не меняет. Они не состоят из сплошных единиц, как можно было бы подумать, а имеют следующую структуру: \[ \left(\begin{array}{cccc} 1 & 0 & \dots & 0\\ 0 & 1\\ \vdots & & \ddots\\ 0 & & & 1 \end{array}\right). \] На главной диагонали у них единицы, а остальные элементы – нули.
Умножение матриц не перестановочно: за редкими исключениями, $AB\neq BA$. К исключениям относятся единичные матрицы: $AE=EA=A$.
Транспонирование
При транспонировании матрицы номера строк новой матрицы являются номерами столбцов старой, и наоборот \[ A^{T}:\qquad a_{ij}^{T}=a_{ji}. \] Графически можно представить происходящее как поворот матрицы на $180^{\circ}$ вокруг главной диагонали, при котором столбцы превращаются в строки: \[ \left(\begin{array}{ccc} \boxed{\begin{array}{c} 1\\ 2\\ 1 \end{array}} & \begin{array}{c} 3\\ 1\\ 3 \end{array} & \begin{array}{c} 1\\ 2\\ 1 \end{array}\end{array}\right)^{T}=\left(\begin{array}{c} \boxed{\begin{array}{ccc} 1 & 2 & 1\end{array}}\\ \begin{array}{ccc} 3 & 1 & 3\end{array}\\ \begin{array}{ccc} 1 & 2 & 1\end{array} \end{array}\right) \] Задание: вычислить \[ \left(\begin{array}{cc} -4 & -1\\ 2 & 1\\ -1 & -1 \end{array}\right)-2\left(\begin{array}{cc} -3 & -2\\ 1 & 0\\ 0 & 1 \end{array}\right) \] \[ \left(\begin{array}{rr} 12 & 1\\ 18 & 0\\ 0 & -15\\ 0 & 18 \end{array}\right)-\left(\begin{array}{rr} 11 & 5\\ -2 & -1\\ 1 & 0\\ 0 & 1 \end{array}\right) \] \[ \left(\begin{array}{ccccc} 2 & 1 & 0 & 0 & 0\\ 1 & 2 & 1 & 0 & 0\\ 0 & 1 & 2 & 1 & 0\\ 0 & 0 & 1 & 2 & 1\\ 0 & 0 & 0 & 1 & 2 \end{array}\right)+\left(\begin{array}{ccccc} 1 & 2 & 2 & 2 & 2\\ 2 & 1 & 2 & 2 & 2\\ 2 & 2 & 1 & 2 & 2\\ 2 & 2 & 2 & 1 & 2\\ 2 & 2 & 2 & 2 & 1 \end{array}\right) \]
Задание: вычислить произведения и степени
Задание: Найти обратные матрицы для следующих матриц: