Несобственные интегралы, зависящие от параметра, и их сходимость
В случае, когда в интеграле присутствует ещё и параметр, от него начинает зависеть не только значение интеграла, но и сам факт его наличия (сходимости). Множество значений параметров, при которых интеграл сходится, называется его областью сходимости. Если параметр один, то это отрезки/интервалы на вещественной оси; но если интервалов становится много – область сходимости оказывается фигурой в более многомерном пространстве.
Пример: № 2362
Исследовать на сходимость интеграл
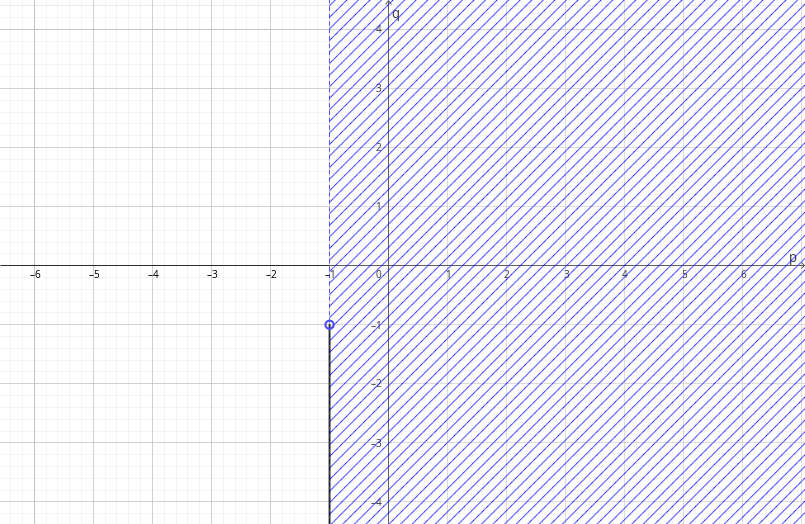
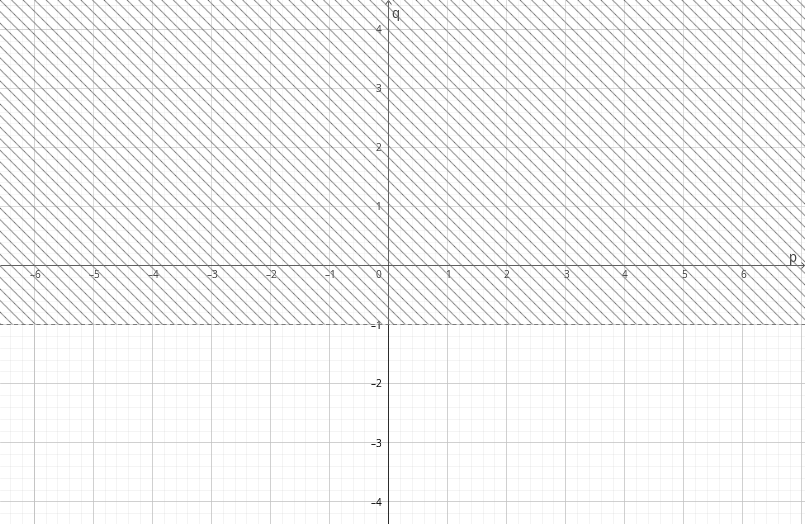
\[ \int\limits_{0}^{1}x^{p}\ln^{q}\frac{1}{x}dx. \] В этом интеграле есть два параметра, и потому «исследовать на сходимость» означает найти область сходимости на плоскости ($p,q$). В зависимости от параметров, подынтегральное выражение может оказаться неопределённым и в нижнем, и в верхнем пределах интегрирования (во внутренних точках области интегрирования оно непрерывно). Разобьём интеграл на два и будем изучать их сходимость отдельно: \begin{equation} \int\limits_{0}^{1}x^{p}\ln^{q}\frac{1}{x}dx=\int\limits_{0}^{1/e}x^{p}\ln^{q}\frac{1}{x}dx+\int\limits_{1/e}^{1}x^{p}\ln^{q}\frac{1}{x}dx.\label{razl} \end{equation}
1. В первом слагаемом заменим переменную: $\ln\frac{1}{x}=t$, $x=e^{-t}$, $dx=-e^{-t}dt$ \[ \int\limits_{0}^{1/e}x^{p}\ln^{q}\frac{1}{x}dx=-\int\limits_{\infty}^{1}\left(e^{-t}\right)^{p}t^{q}e^{-t}dt=\int\limits_{1}^{\infty}e^{-\left(p+1\right)t}t^{q}dt. \]
а) Пусть $p+1 > 0$ ($p > -1$). Сравним подынтегральное выражение с функцией $e^{-\frac{p+1}{2}t}$ (нам пригодится, что и $\frac{p+1}{2} > 0$) \[ \lim_{t\to\infty}\frac{e^{-\left(p+1\right)t}t^{q}}{e^{-\frac{p+1}{2}t}}=\lim_{t\to\infty}e^{-\frac{p+1}{2}t}t^{q}=0. \] Так как числитель и знаменатель положительны, по признаку сравнения IIб из сходимости знаменателя следует сходимость числителя. Знаменатель сходится: \[ \int\limits_{1}^{\infty}e^{-\frac{p+1}{2}t}dt=-\left.\frac{2}{p+1}e^{-\frac{p+1}{2}t}\right|_{1}^{\infty}=\frac{2}{p+1}, \] а значит, сходится и числитель. Итак, при $p > -1$ первое слагаемое сходится.
б) Пусть $p+1 < 0$ ($p < -1$). Тогда $-\left(p+1\right) > 0$, \[ \lim_{t\to\infty}\frac{t^{-q}}{e^{-\left(p+1\right)t}}=0 \] при любом $-q$ в силу № 60 из Демидовича, а тогда \[ \lim_{t\to\infty}e^{-\left(p+1\right)t}t^{q}=\lim_{t\to\infty}\left(\frac{t^{-q}}{e^{-\left(p+1\right)t}}\right)^{-1}=\infty \] По определению предела это означает, что есть такое $T$, что при всяком $t > T$ \[ e^{-\left(p+1\right)t}t^{q} > 1 \] Но тогда \[ \int\limits_{T}^{\infty}1dt=\lim_{b\to\infty}\int\limits_{T}^{b}1dt=\lim_{b\to\infty}b-T=\infty, \] интеграл меньшей единицы расходится на бесконечности, значит и интеграл от большего $\int\limits_{T}^{\infty}e^{-\left(p+1\right)t}t^{q}dt$ расходится по I признаку сравнения. Нужный нам интеграл можно разложить \[ \int\limits_{1}^{\infty}e^{-\left(p+1\right)t}t^{q}dt=\int\limits_{1}^{T}e^{-\left(p+1\right)t}t^{q}dt+\int\limits_{T}^{\infty}e^{-\left(p+1\right)t}t^{q}dt, \] и тут первое слагаемое – собственный интеграл, второе – расходящийся; значит, их сумма также расходится (сумма существует, когда существуют все её слагаемые). Итак, при $p < -1$ первое слагаемое расходится.
в) Наконец, пусть $p=-1$. \[ \int\limits_{1}^{\infty}e^{-\left(p+1\right)t}t^{q}dt=\int\limits_{1}^{\infty}t^{q}dt=\left.\frac{t^{q+1}}{q+1}\right|_{1}^{\infty}=\left\{ \begin{array}{ll} 0, & q+1 < 0,\\ \infty, & q+1 > 0. \end{array}\right. \] Остался неисследованным только случай, когда $q+1=0$: \[ \int\limits_{1}^{\infty}t^{q}dt=\int\limits_{1}^{\infty}t^{-1}dt=\left.\ln\left|t\right|\right|_{1}^{\infty}=\infty. \] Конечный результат при $p=-1$ получается (а значит, интеграл сходится) при $q+1 < 0$, т.е. при $q < -1$.
Итогом первого пункта будет то, что интеграл вида
\[ \int\limits_{0}^{1/e}x^{p}\ln^{q}\frac{1}{x}dx=\int\limits_{1}^{\infty}e^{-\left(p+1\right)t}t^{q}dt \] сходится при $p > -1$ и $\forall q$; а ещё при $p=-1$ и $q < -1$.
2. Мы получили область сходимости первого слагаемого в (\ref{razl}), теперь займёмся вторым. Заменим переменную: $\ln^{-1}\frac{1}{x}=s$, $\ln\frac{1}{x}=\frac{1}{s}$, $x=e^{-1/s}$, $dx=e^{-1/s}\frac{ds}{s^{2}}$: \[ \int\limits_{1/e}^{1}x^{p}\ln^{q}\frac{1}{x}dx=\int\limits_{1}^{\infty}\left(e^{-1/s}\right)^{p}\left(\frac{1}{s}\right)^{q}e^{-1/s}\frac{ds}{s^{2}}=\int\limits_{1}^{\infty}e^{-\frac{p+1}{s}}s^{-q-2}ds. \] Возьмём функцию $s^{-q-2}$ и вычислим предел \[ \lim_{s\to\infty}\frac{e^{-\frac{p+1}{s}}s^{-q-2}}{s^{-q-2}}=\lim_{s\to\infty}e^{-\frac{p+1}{s}}=e^{0}=1\neq0, \] так как числитель и знаменатель положительны – интегралы от обеих функций ведут себя одинаково по II признаку сравнения. Что даёт интеграл знаменателя: \[ \int\limits_{1}^{\infty}s^{-q-2}ds=\left\{ \begin{array}{ll} 0, & -q-1 < 0,\\ \infty, & -q-1=0,\\ \infty, & -q-1 > 0. \end{array}\right. \] Он сходится при $-q-1 < 0$ ($q > -1$) и при любом $p$.
Теперь у нас есть область сходимости и для второго слагаемого. Однако весь интеграл (\ref{razl}) сходится там, где сходятся оба его слагаемых; иначе, его область сходимости есть пересечение областей сходимости слагаемых
Задание: найдите область сходимости для интегралов в № 2361, 2363, 2369, 3741.
Помимо сходимости простой есть ещё сходимость равномерная.
Напомню: говорят, что функция $f\left(x,y\right)$ стремится к функции $\varphi\left(x\right)$ при $y\to\infty$ и при $x$ лежащем в множестве $\mathcal{X}$, \[ \lim_{y\to\infty}f\left(x,y\right)=\varphi\left(x\right), \] если для $\forall\varepsilon > 0$ и $\forall x\in\mathcal{X}$ $\exists Y$, что при $\forall y > Y$ $\Longrightarrow$ \[ \left|f\left(x,y\right)-\varphi\left(x\right)\right| < \varepsilon. \] Это обычное определение предела, известное с первого курса. Но говорят также, что функция $f\left(x,y\right)$ равномерно стремится к функции $\varphi\left(x\right)$ на множестве $\mathcal{X}$ при $y\to\infty$, если выполняется определение, дополненное в одном месте. А именно, для $\forall\varepsilon > 0$ $\exists Y$, что при $\forall y > Y$ и $\forall x\in\mathcal{X}$ $\Longrightarrow$ \[ \left|f\left(x,y\right)-\varphi\left(x\right)\right| < \varepsilon. \] Разница в том, что в первом случае при разных $x$ итоговое неравенство начинало выполняться начиная с разных $Y$, а тут есть такой достаточно большой $Y$, начиная с которого оно начинает выполняться для любого $x$ из рассматриваемого множества $\mathcal{X}$. Ещё можно сформулировать так: при обычной сходимости множество пороговых $Y$ не обязано было иметь верхней грани, а при равномерной – обязано.
Если теперь вместо произвольной функции $f\left(x,y\right)$ подставить интеграл с параметром $y$ – мы получим определение равномерной сходимости интеграла: интеграл \[ \int\limits_{a}^{\infty}f\left(x,y\right)dy=\lim_{b\to\infty}\int\limits_{a}^{b}f\left(x,y\right)dy=\varphi\left(x\right) \] называется равномерно сходящимся при $\forall x\in\mathcal{X}$, если для $\forall\varepsilon > 0$ $\exists B$, что при $\forall b > B$ и $\forall x\in\mathcal{X}$ $\Longrightarrow$ \[ \left|\int\limits_{a}^{b}f\left(x,y\right)dy-\varphi\left(x\right)\right| < \varepsilon. \]
Равномерная сходимость нужна нам потому, что она позволяет делать с интегралами некоторые привычные действия. Например, в равномерно сходящийся интеграл можно вносить интеграл по параметру. А ещё можно вносить производную по параметру и применять её к подынтегральному выражению – но если равномерно сходится интеграл уже от подынтегрального выражения.
Проверяется равномерная сходимость при помощи критерия Коши. Вспомним, как он выглядел для функций: функция $f\left(x,y\right)$ равномерно стремится к функции $\varphi\left(x\right)$ на множестве $\mathcal{X}$ при $y\to\infty$ тогда и только тогда, когда для $\forall\varepsilon > 0$ $\exists Y$, что при $\forall y_{1},y_{2} > Y$ и $\forall x\in\mathcal{X}$ $\Longrightarrow$ \[ \left|f\left(x,y_{2}\right)-f\left(x,y_{1}\right)\right| < \varepsilon. \] В применении к интегралам это определение выглядит так: интеграл $\int\limits_{a}^{\infty}f\left(x,y\right)dy$ сходится равномерно на множестве $\mathcal{X}$ тогда и только тогда, когда для $\forall\varepsilon > 0$ $\exists B$, что при $\forall b_{1},b_{2} > B$ и $\forall x\in\mathcal{X}$ $\Longrightarrow$ \[ \left|\int\limits_{a}^{b_{2}}f\left(x,y\right)dy-\int\limits_{a}^{b_{1}}f\left(x,y\right)dy\right|=\left|\int\limits_{b_{1}}^{b_{2}}f\left(x,y\right)dy\right| < \varepsilon. \] Критерий Коши неудобен, но действует в обе стороны, и хорош тогда, когда надо доказать отсутствие равномерной сходимости – а такая задача тоже может возникнуть.
В одну сторону действует признак Вейерштрасса. Он гласит следующее: интеграл $\int\limits_{a}^{\infty}f\left(x,y\right)dy$ сходится равномерно на множестве $\mathcal{X}$, если существует такая функция $g\left(y\right)$, которая
0) не зависит от $x$ (этот пункт следует из записи $g\left(y\right)$, но его там мало кто видит),
1) при $\forall x\in\mathcal{X}$ и $y > a$ удовлетворяет неравенству $\left|f\left(x,y\right)\right| < g\left(y\right)$,
2) имеет сходящийся интеграл $\int\limits_{a}^{\infty}g\left(y\right)dy$ .
Пример: № 3757 Исследовать на равномерную сходимость в указанных промежутках следующий интеграл: \[ \int\limits_{1}^{\infty}x^{\alpha}e^{-x}dx,\qquad a\leqslant\alpha\leqslant b \] При $a > 1$ $a^{x}$ – возрастающая функция, поэтому из того, что $x > 1$ и $\alpha\leqslant b$ следует что $x^{\alpha}\leqslant x^{b}$, а значит, \[ x^{\alpha}e^{-x}\leqslant x^{b}e^{-x} \] при $\forall\alpha\in\left[a,b\right]$, причём мажорирующая функция $x^{b}e^{-x}$ не зависит от $\alpha$. Это уже половина признака Вейерштрасса. Осталось доказать, что сходится интеграл $\int\limits_{1}^{\infty}x^{b}e^{-x}dx$. Выберем функцию $e^{-x/2}$ и вычислим предел \[ \lim_{x\to\infty}\frac{x^{b}e^{-x}}{e^{-x/2}}=\lim_{x\to\infty}\frac{x^{b}}{e^{x/2}}=0, \] который позволит применить признак IIб.
Вычислим интеграл \[ \int\limits_{1}^{\infty}e^{-x/2}dx=\left.-2e^{-x/2}\right|_{0}^{\infty}=-2\left(0-1\right)=2 \] и убедимся, что он сходится. Тогда вместе с ним, по признаку IIб сходится интеграл $\int\limits_{1}^{\infty}x^{b}e^{-x}dx$, а из этого, по признаку Вейерштрасса, равномерно сходится интеграл $\int\limits_{1}^{\infty}x^{\alpha}e^{-x}dx$ при $\alpha$, лежащем на интервале $\left[a,b\right]$.
Пример: № 3759 \begin{equation} \int\limits_{1}^{\infty}\frac{dx}{\left(x-\alpha\right)^{2}+1},\qquad0\leqslant\alpha\label{int3759} \end{equation} Начнём с того, что просто сходимость у этого интеграла есть: \[ \int\limits_{1}^{\infty}\frac{dx}{\left(x-\alpha\right)^{2}+1}=\left.\mathrm{arctg}\,\left(x-\alpha\right)\right|_{0}^{\infty}=\frac{\pi}{2}+\mathrm{arctg}\,\alpha. \] Но с равномерной сходимостью всё обстоит хуже. При $x=\alpha$ \[ \frac{1}{\left(x-\alpha\right)^{2}+1}=1, \] так что замажорировать подынтегральное выражение можно только функцией, всюду большей чем 1; а от такой функции интеграл сходиться не будет. Признак Вейерштрасса применить не получится, и возникает подозрение, что равномерной сходимостью этот интеграл вовсе не обладает. Но неприменимость признака Вейерштрасса доказательством отсутствия равномерной сходимости не является, и придётся отдуваться другими методами.
Интеграл $\int\limits_{a}^{\infty}f\left(x,y\right)dy$ не обладает равномерной сходимостью на множестве $\mathcal{X}$, если не выполняется критерий Коши: когда есть такое $\varepsilon > 0$, что при $\forall B$ найдутся такие $b_{1},b_{2} > B$ и $x\in\mathcal{X}$, для которых \[ \left|\int\limits_{b_{1}}^{b_{2}}f\left(x,y\right)dy\right|\geqslant\varepsilon. \] В нашем случае, если есть такие $\varepsilon > 0$, что при $\forall X$ найдутся такие $b_{1},b_{2} > X$ и $\alpha\geqslant0$, для которых \[ \left|\int\limits_{b_{1}}^{b_{2}}\frac{dx}{\left(x-\alpha\right)^{2}+1}\right|\geqslant\varepsilon. \] Докажем, что в данном случае такое $\varepsilon$ есть. Для произвольного $X$ выберем $\alpha=X+2$, $b_{1}=\alpha-1=X+1$ и $b_{2}=\alpha+1$. \[ \int\limits_{b_{1}}^{b_{2}}\frac{dx}{\left(x-\alpha\right)^{2}+1}=\mathrm{arctg}\,\left(1\right)-\mathrm{arctg}\,\left(-1\right)=\frac{\pi}{4}-\left(-\frac{\pi}{4}\right)=\frac{\pi}{2} \] Следовательно, если мы выберем $\varepsilon=\frac{\pi}{4}$, то \[ \left|\int\limits_{b_{1}}^{b_{2}}\frac{dx}{\left(x-\alpha\right)^{2}+1}\right|=\frac{\pi}{2}\geqslant\frac{\pi}{4}=\varepsilon, \] что и требовалось. Таким образом, при $\alpha\geqslant0$ интеграл (\ref{int3759}) равномерной сходимостью не обладает по критерию Коши.
Задание: № 3756, 3758, 3760.