На этом занятии мы от пределов последовательностей перейдём к пределам функций от непрерывного аргумента.

Определения и примеры

У нас будет очень много определений. Начнём с тех из них, которые знакомы по последовательностям.

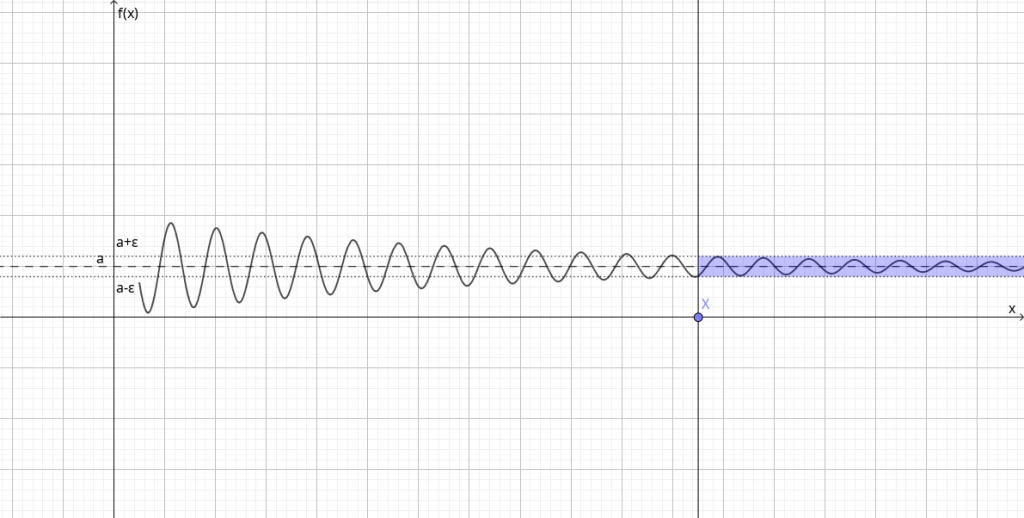
Определение 1. Число $a$ называется пределом функции $f\left(x\right)$ при $x$ стремящемся к бесконечности, если для любого, сколь угодно малого, числа $\varepsilon > 0$ найдётся такое число $X\left(\varepsilon\right)$, что все значения $f\left(x\right)$ при $x > X\left(\varepsilon\right)$, удовлетворяют неравенству: $\left|f\left(x\right)-a\right| < \varepsilon$. При этом говорят, что функция стремится к числу $a$ на бесконечности, и пишут \[ \lim_{x\to\infty}f\left(x\right)=a. \] Графически это можно представить так:

Как бы узок ни был коридор вокруг числа $a$, график функции, стремящейся к этому числу, рано или поздно (после определённого $X$) окажется в этом коридоре навсегда.

Определение 2. Функция $f\left(x\right)$ называется стремящейся к бесконечности при $x$ стремящемся к бесконечности, если для любого числа $E$ найдётся такое число $X\left(E\right)$, что все значения $f\left(x\right)$ при $x > X\left(E\right)$ удовлетворяют неравенству: $f\left(x\right) > E$. В этом случае пишут \[ \lim_{x\to\infty}f\left(x\right)=\infty. \]

Определение 3. Функция $f\left(x\right)$ называется стремящейся к минус бесконечности при $x$ стремящемся к бесконечности, если для любого числа $E$ найдётся такое число $X\left(E\right)$, что все значения $f\left(x\right)$ при $x > X\left(E\right)$ удовлетворяют неравенству: $f\left(x\right) < E$. В этом случае пишут \[ \lim_{x\to\infty}f\left(x\right)=-\infty. \]

Всё ещё верны (и по почти тем же причинам) выведенные для последовательностей пределы: \begin{equation} \lim_{x\to\infty}\frac{1}{x^{\alpha}}=\lim_{x\to\infty}q^{x}=0,\qquad\alpha > 0,\;0 < q < 1.\label{steps} \end{equation} Но, в отличие от натурального номера элемента последовательности, переменная $x$ может не иметь наименьшего значения. Отсюда вытекают ещё три определения.

Определение 4. Число $a$ называется пределом функции $f\left(x\right)$ при $x$ стремящемся к минус бесконечности, если для любого, сколь угодно малого, числа $\varepsilon > 0$ найдётся такое число $X\left(\varepsilon\right)$, что все значения $f\left(x\right)$ при $x < X\left(\varepsilon\right)$, удовлетворяют неравенству: $\left|f\left(x\right)-a\right| < \varepsilon$. При этом говорят, что функция стремится к числу $a$ на минус бесконечности, и пишут \[ \lim_{x\to-\infty}f\left(x\right)=a. \] Представить себе происходящее можно, развернув график на рис. 1 слева направо.

Определение 5. Функция $f\left(x\right)$ называется стремящейся к бесконечности при $x$ стремящемся к минус бесконечности, если для любого числа $E$ найдётся такое число $X\left(E\right)$, что все значения $f\left(x\right)$ при $x < X\left(E\right)$ удовлетворяют неравенству: $f\left(x\right) > E$. В этом случае пишут \[ \lim_{x\to-\infty}f\left(x\right)=\infty. \]

Определение 6. Функция $f\left(x\right)$ называется стремящейся к минус бесконечности при $x$ стремящемся к минус бесконечности, если для любого числа $E$ найдётся такое число $X\left(E\right)$, что все значения $f\left(x\right)$ при $x < X\left(E\right)$ удовлетворяют неравенству: $f\left(x\right) < E$. В этом случае пишут \[ \lim_{x\to-\infty}f\left(x\right)=-\infty. \]

А вот дальше начнутся определения, не имевшие среди последовательностей аналогов. Новые понятия появляются потому, что целая переменная не может неограниченно приближаться к конечному значению: между 1 и 0 нет целых чисел. А дробная, и тем более вещественная – может. Например, можно сколько угодно последовательно делить число на 2, и результатом будут всё более близкие к нулю значения.

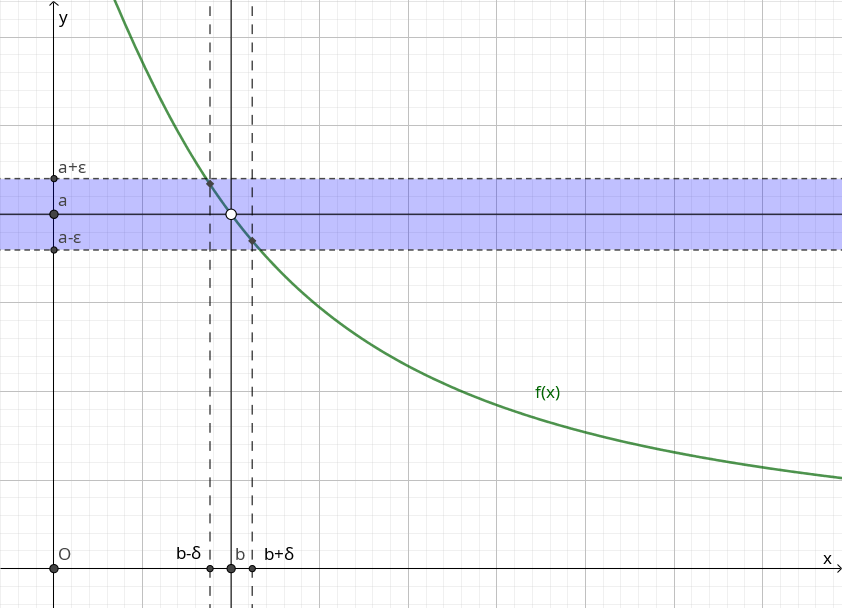
Определение 7. Число $a$ называется пределом функции $f\left(x\right)$ при $x$ стремящемся к $b$, если для любого, сколь угодно малого, числа $\varepsilon > 0$ найдётся такое число $\delta$, что если $\left|x-b\right| < \delta$, то $\left|f\left(x\right)-a\right| < \varepsilon$. При этом говорят, что функция стремится к числу $a$ при $x$ стремящемся к $b$, и пишут \[ \lim_{x\to b}f\left(x\right)=a. \]

Пример: Докажем, что \begin{equation} \lim_{x\to1}\sqrt{x}=1.\label{limsqrt} \end{equation} Тут $a=b=1$, $f\left(x\right)=\sqrt{x}$. Из определения следует, что доказать мы должны наличие для всякого $\varepsilon > 0$ такого $\delta$, что при $\left|x-b\right| < \delta$ выполнится $\left|\sqrt{x}-1\right| < \varepsilon$.

Рассмотрим сначала произвольные $0 < \varepsilon < 1$ (это не всё множество $\varepsilon$, которое мы должны рассмотреть, но начнём с этого подмножества). Тогда \[ \varepsilon^{2} < \varepsilon < 2\varepsilon, \] \[ 2\varepsilon-\varepsilon^{2} > 0. \] Выберем $\delta=2\varepsilon-\varepsilon^{2}$. Тогда из $\left|x-1\right| < \delta$ имеем \[ \left|x-1\right| < 2\varepsilon-\varepsilon^{2}, \] \[ -2\varepsilon+\varepsilon^{2} < x-1 < 2\varepsilon-\varepsilon^{2} < 2\varepsilon+\varepsilon^{2}, \] \[ 1-2\varepsilon+\varepsilon^{2} < x < 1+2\varepsilon+\varepsilon^{2}, \] \[ 0\leqslant\left(1-\varepsilon\right)^{2} < x < \left(1+\varepsilon\right)^{2}, \] \[ 1-\varepsilon < \sqrt{x} < 1+\varepsilon, \] \[ -\varepsilon < \sqrt{x}-1 < \varepsilon, \] \[ \left|\sqrt{x}-1\right| < \varepsilon. \] Для $\varepsilon$, меньших единицы, нужное неравенство мы доказали.

Возьмём теперь $\varepsilon\geqslant1$. Выберем любое $0 < \gamma < 1$ (например, $\gamma=\frac{1}{2}$), и построим для него $\delta=2\gamma-\gamma^{2}$. Тогда \[ \left|\sqrt{x}-1\right| < \gamma < 1\leqslant\varepsilon, \] откуда $\left|\sqrt{x}-1\right| < \varepsilon$. Теперь мы доказали, что для совсем любого положительного $\varepsilon$ можно выбрать требуемое $\delta$, значит, (\ref{limsqrt}) верно. Кстати, значение функции $f\left(x\right)=\sqrt{x}$ при $x=1$ тоже равно 1. Функции, у которых предел в некоторой точке равен значению функции в ней же, называются непрерывными в этой точке. Сейчас мы доказали непрерывность квадратного корня в единице.

Для следующего примера докажем одно важное свойство.

Если для функция $f\left(x\right)$ непрерывна в точке $b$ (т.е. $\lim\limits_{x\to b}f\left(x\right)=f\left(b\right)$), а функция $g\left(x\right)$ равна $f\left(x\right)$ при любом $x\neq b$, то \begin{equation} \lim_{x\to b}g\left(x\right)=f\left(b\right)=\lim\limits_{x\to b}f\left(x\right).\label{svvo} \end{equation} В самом деле, раз \[ \lim_{x\to b}f\left(x\right)=f\left(b\right), \] то для всякого $\varepsilon > 0$ существует такое $\delta$, что если $\left|x-b\right| < \delta$, то \[ \left|f\left(x\right)-f\left(b\right)\right| < \varepsilon. \] Но при $x\neq b$ $f\left(x\right)=g\left(x\right)$, а значит, при тех же $\varepsilon > 0$, $\delta$ и $x$ \[ \left|g\left(x\right)-f\left(b\right)\right| < \varepsilon, \] откуда по определению 7 следует (\ref{svvo}).

Пример: найти предел \[ \lim_{x\to1}\frac{\left(x-1\right)\left(x+2\right)}{x-1}. \] В нашем случае \[ g\left(x\right)=\frac{\left(x-1\right)\left(x+2\right)}{x-1}, \] и эта функция не определена при $x=1$ (на ноль делить нельзя). Но при $x\neq1$ \[ \frac{\left(x-1\right)\left(x+2\right)}{x-1}=x+2=f\left(x\right). \] Доказательство непрерывности $f\left(x\right)=x+2$ в точке 1 оставлю вам. Отсюда и по свойству (\ref{svvo}), \[ \lim_{x\to1}\frac{\left(x-1\right)\left(x+2\right)}{x-1}=\lim_{x\to1}\left(x+2\right)=3. \]

Не всегда, однако, в точке, к которой стремится аргумент функции, существует и значение функции.

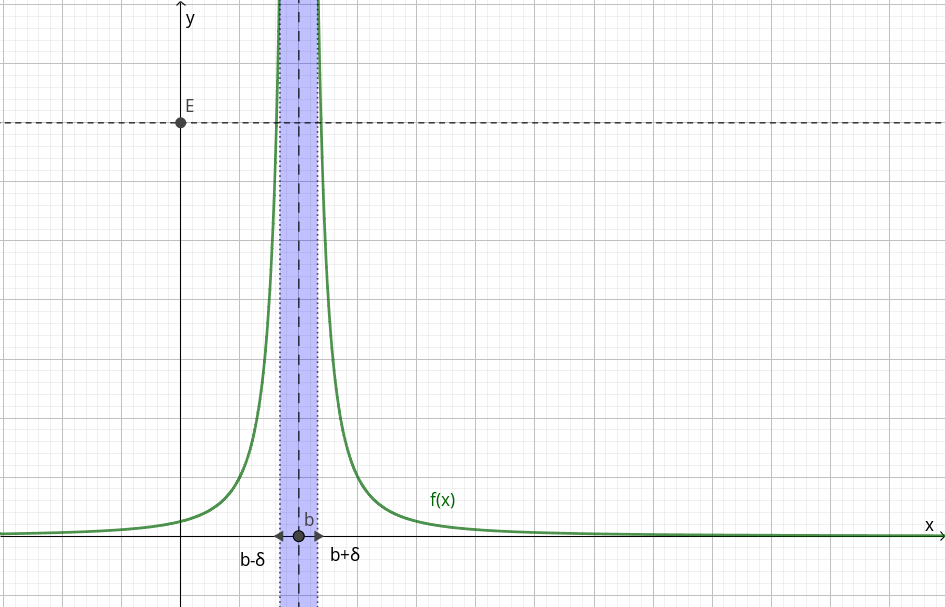
Определение 8. Функция $f\left(x\right)$ называется стремящейся к бесконечности при $x$ стремящемся к $b$, если для любого числа $E$ найдётся такое число $\delta$, что если $\left|x-b\right| < \delta$, то $f\left(x\right) > E$. В этом случае пишут \[ \lim_{x\to b}f\left(x\right)=\infty. \]

Пример: \[ \lim_{x\to0}\frac{1}{x^{2}}=\infty. \] В самом деле, для любого $E > 0$ возьмём $\delta=\frac{1}{\sqrt{E}}$. Тогда при $\left|x-0\right| < \delta$ \[ \left|x\right| < \frac{1}{\sqrt{E}}, \] \[ x^{2} < \frac{1}{E}, \] \[ \frac{1}{x^{2}} > E. \] при $E \leqslant 0$ построим аналогичное $\delta$ для единицы. Тогда \[ \frac{1}{x^{2}} > 1 > E. \]

Определение 9. Функция $f\left(x\right)$ называется стремящейся к бесконечности при $x$ стремящемся к $b$, если для любого числа $E$ найдётся такое число $\delta$, что если $\left|x-b\right| < \delta$, то $f\left(x\right) < E$. В этом случае пишут \[ \lim_{x\to b}f\left(x\right)=-\infty. \]

Существуют также т.н. односторонние пределы (предел слева и справа), возникающие при стремлении $x$ к $b$ с одной (соответствующей) стороны. Для бесконечностей их не было, поскольку к каждой бесконечности можно приближаться только с одной стороны: к $+\infty$ – слева, а к $-\infty$ - справа. Определения этих пределов получаются из вышеприведённых, если заменить условие $\left|x-b\right| < \delta$ (при котором $b-\delta < x < b+\delta$ и область для $x$ симметрична), на условие $b < x < b+\delta$ для правого предела и $b-\delta < x < b$ для левого. Каждый сможет составить эти определения самостоятельно, так что я не буду добавлять в текст ещё шесть штук определений.

Если в точке существует предел (назовём его для этого случая «общий предел»), равный $a$, то в той же точке существуют и левый, и правый пределы, и они оба равны $a$. Обратно, если в точке хоть один из односторонних пределов не существует, или оба существуют, но друг другу не равны, то предела в этой точке нет.

Свойства и опять примеры

Остаются верны для конечных пределов функций (как при $x\to b$, так и при $x\to\infty$) свойства, до этого вводившиеся для пределов последовательностей:

0) Если $C=const$, \begin{equation} \lim\limits C=C.\label{limC} \end{equation}

1) Если существуют $\lim\limits f\left(x\right)$ и $\lim\limits g\left(x\right)$,

а) то существует $\lim\limits\left[f\left(x\right)\pm g\left(x\right)\right]$, при этом \begin{equation} \lim\limits\left[f\left(x\right)\pm g\left(x\right)\right]=\lim\limits f\left(x\right)\pm\lim\limits g\left(x\right);\label{limsum} \end{equation}

б) существует $\lim\limits\left[f\left(x\right)g\left(x\right)\right]$, при этом \begin{equation} \lim\limits\left[f\left(x\right)g\left(x\right)\right]=\lim\limits f\left(x\right)\cdot\lim\limits g\left(x\right);\label{limpr} \end{equation}

в) если к тому же $g\left(x\right)\neq0$ и $\lim\limits g\left(x\right)\neq0$, существует $\lim\limits\frac{f\left(x\right)}{g\left(x\right)}$ и \begin{equation} \lim\limits\frac{f\left(x\right)}{g\left(x\right)}=\frac{\lim\limits f\left(x\right)}{\lim\limits g\left(x\right)}.\label{limdr} \end{equation}

2) Если $\lim\limits f\left(x\right)=0$ и $g\left(x\right)$ ограничена, то $\lim\limits f\left(x\right)g\left(x\right)=0$.

3) Если $\lim\limits f\left(x\right)=a$ и $\lim\limits h\left(x\right)=a$ , причём $f\left(x\right)\leqslant g\left(x\right)\leqslant h\left(x\right)$, то $\lim\limits g\left(x\right)=a$ .

Элементарные функции непрерывны во всех точках, кроме известных разрывов (доказательства делаются похоже на случай корня, тут их приводить не будем). Сумма и произведение элементарных функций непрерывны, дробь с непрерывными функциями непрерывна кроме нулей знаменателя. Композиция функций $f(g(x))$ непрерывна в точке $x$, если $g(x)$ непрерывна в точке $x$ и $f$ непрерывна в точке $g(x)$.

Пример: № 411 Пункты отличаются только тем, к чему стремится $x$.

а) \[ \lim\limits_{x\to0}\frac{x^{2}-1}{2x^{2}-x-1} \] Числитель и знаменатель – полиномы, они непрерывны. Знаменатель в нуле не равен нулю, значит, можно вносить предел в дробь. Непрерывность полиномов позволяет в них сразу подставлять аргумент для получения предела: \[ \lim\limits_{x\to0}\frac{x^{2}-1}{2x^{2}-x-1}=\frac{\lim\limits_{x\to0}\left(x^{2}-1\right)}{\lim\limits_{x\to0}\left(2x^{2}-x-1\right)}=\frac{\left.\left(x^{2}-1\right)\right|_{x=0}}{\left.\left(2x^{2}-x-1\right)\right|_{x=0}}=\frac{-1}{-1}=1 \]

б) \[ \lim\limits_{x\to1}\frac{x^{2}-1}{2x^{2}-x-1} \] Тут возникает проблема со знаменателем: $\left.\left(2x^{2}-x-1\right)\right|_{x=1}=2-1-1=0$. Но мы преобразуем функцию: \[ \frac{x^{2}-1}{2x^{2}-x-1}=\frac{\left(x-1\right)\left(x+1\right)}{\left(x-1\right)\left(2x+1\right)}= \] При $x\neq1$ \[ =\frac{x+1}{2x+1}. \] Тогда \[ \lim\limits_{x\to1}\frac{x^{2}-1}{2x^{2}-x-1}=\lim\limits_{x\to1}\frac{x+1}{2x+1}=\left.\left(\frac{x+1}{2x+1}\right)\right|_{x=1}=\frac{2}{3}. \]

в) \[ \lim\limits_{x\to\infty}\frac{x^{2}-1}{2x^{2}-x-1} \] Числитель и знаменатель, стремящиеся к бесконечности, нас, конечно, не устраивают. Но мы разделим числитель и знаменатель на $x^{2}$: \[ \frac{x^{2}-1}{2x^{2}-x-1}=\frac{1-\frac{1}{x^{2}}}{2-\frac{1}{x}-\frac{1}{x^{2}}} \] По формуле (\ref{steps}), так как $2 > 0$ и $1 > 0$, \[ \lim\limits_{x\to\infty}\frac{1}{x^{2}}=\lim\limits_{x\to\infty}\frac{1}{x}=0, \] \[ \lim\limits_{x\to\infty}\frac{x^{2}-1}{2x^{2}-x-1}=\lim\limits_{x\to\infty}\frac{1-\frac{1}{x^{2}}}{2-\frac{1}{x}-\frac{1}{x^{2}}}=\frac{\lim\limits_{x\to\infty}\left(1-\frac{1}{x^{2}}\right)}{\lim\limits_{x\to\infty}\left(2-\frac{1}{x}-\frac{1}{x^{2}}\right)}=\frac{\lim\limits_{x\to\infty}1-\lim\limits_{x\to\infty}\frac{1}{x^{2}}}{\lim\limits_{x\to\infty}2-\lim\limits_{x\to\infty}\frac{1}{x}-\lim\limits_{x\to\infty}\frac{1}{x^{2}}}=\frac{1-0}{2-0-0}=\frac{1}{2}. \] В целом, если $x\to \infty$, а предел надо найти от рациональной функции (т.е. отношения полиномов), то делить надо на старшую степень знаменателя: тогда знаменатель будет иметь конечный, но не нулевой предел.

Задание: № 415, 416.

Задание: № 412, 413, 418, 420, 423.

Задание: № 424.1*, 427*.