Добавим ещё одно измерение.
Тройные интегралы берутся по трёхмерным телам и от функций, заданных в пространстве. Они обладают общими для интегралов свойствами аддитивности \[ \iiint\limits_{V}f\left(x,y,z\right)dxdydz=\iiint\limits_{V_{1}}f\left(x,y,z\right)dxdydz+\iiint\limits_{V_{2}}f\left(x,y,z\right)dxdydz, \] и линейности \[ \iiint\limits_{V}\left[\alpha f\left(x,y,z\right)+\beta g\left(x,y,z\right)\right]dxdydz=\alpha\iiint\limits_{V}f\left(x,y,z\right)dxdydz+\beta\iiint\limits_{V}g\left(x,y,z\right)dxdydz. \]
Тройной интеграл сводится к трём однократным интегралам, вложенным друг в друга. При этом для внешнего интеграла пределы не зависят от переменных, для среднего – могут зависеть от переменной интегрирования для внешнего интеграла, для внутреннего – от переменных интегрирования остальных интегралов: \[ \iiint\limits_{V}f\left(x,y,z\right)dxdy=\int\limits_{a}^{b}dx\int\limits_{\alpha(x)}^{\beta(x)}dy\int\limits_{\varphi(x,y)}^{\psi(x,y)}dzf\left(x,y,z\right). \]
Замена старых переменных на новые задаётся системой уравнений замены \[ \left\{ \begin{array}{c} x=x\left(u,v,w\right),\\ y=y\left(u,v,w\right),\\ z=z\left(u,v,w\right); \end{array}\right. \] и производится по формуле \[ \iiint\limits_{V}f\left(x,y,z\right)dxdydz=\iiint\limits_{\Upsilon}f\left(x(u,v),y(u,v),z(u,v,w)\right)\left|J\right|dudvdw, \] где $J$ – якобиан \[ J=\left|\begin{array}{ccc} \frac{\partial x}{\partial u} & \frac{\partial x}{\partial v} & \frac{\partial x}{\partial w}\\ \frac{\partial y}{\partial u} & \frac{\partial y}{\partial v} & \frac{\partial y}{\partial w}\\ \frac{\partial z}{\partial u} & \frac{\partial z}{\partial v} & \frac{\partial z}{\partial w} \end{array}\right|,\qquad\frac{1}{J}=\left|\begin{array}{ccc} \frac{\partial u}{\partial x} & \frac{\partial u}{\partial y} & \frac{\partial u}{\partial z}\\ \frac{\partial v}{\partial x} & \frac{\partial v}{\partial y} & \frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x} & \frac{\partial w}{\partial y} & \frac{\partial w}{\partial z} \end{array}\right|. \]
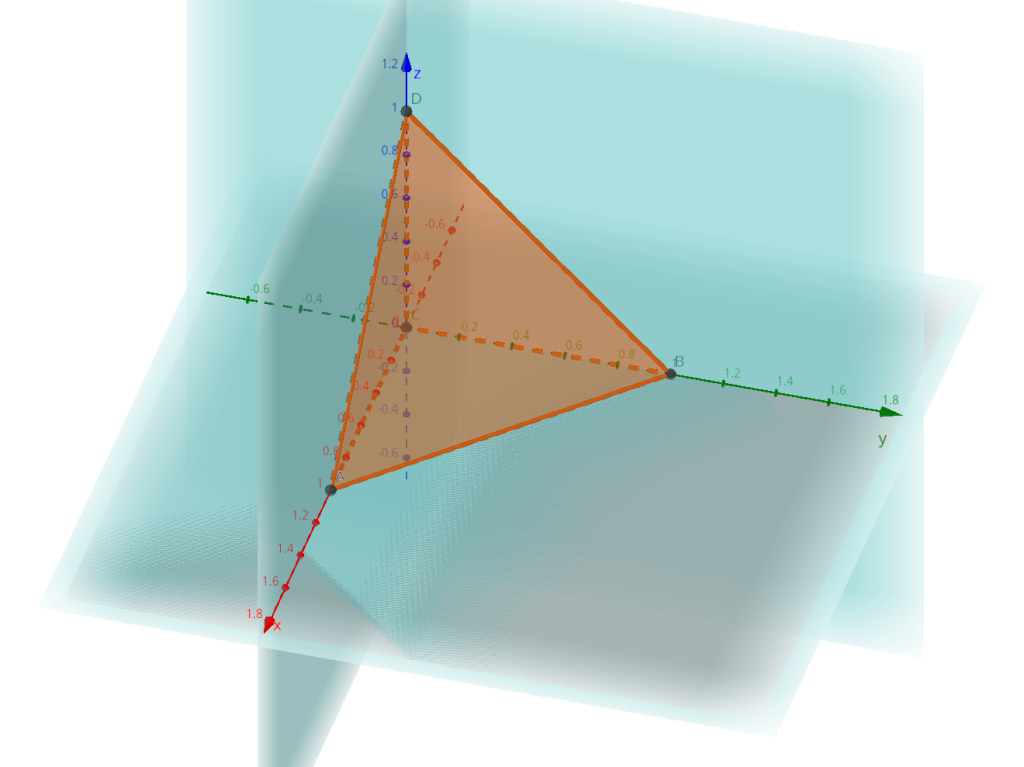
Пример: № 4077 Вычислить интеграл \[ \iiint\limits_{V}\frac{dxdydz}{\left(1+x+y+z\right)^{3}}, \] где область $V$ ограничена поверхностями $x+y+z=1$, $x=0$, $y=0$, $z=0$.
Построим область интегрирования. Последние три поверхности – координатные плоскости, первая – наклонная плоскость. Эти плоскости делят пространство на много частей.
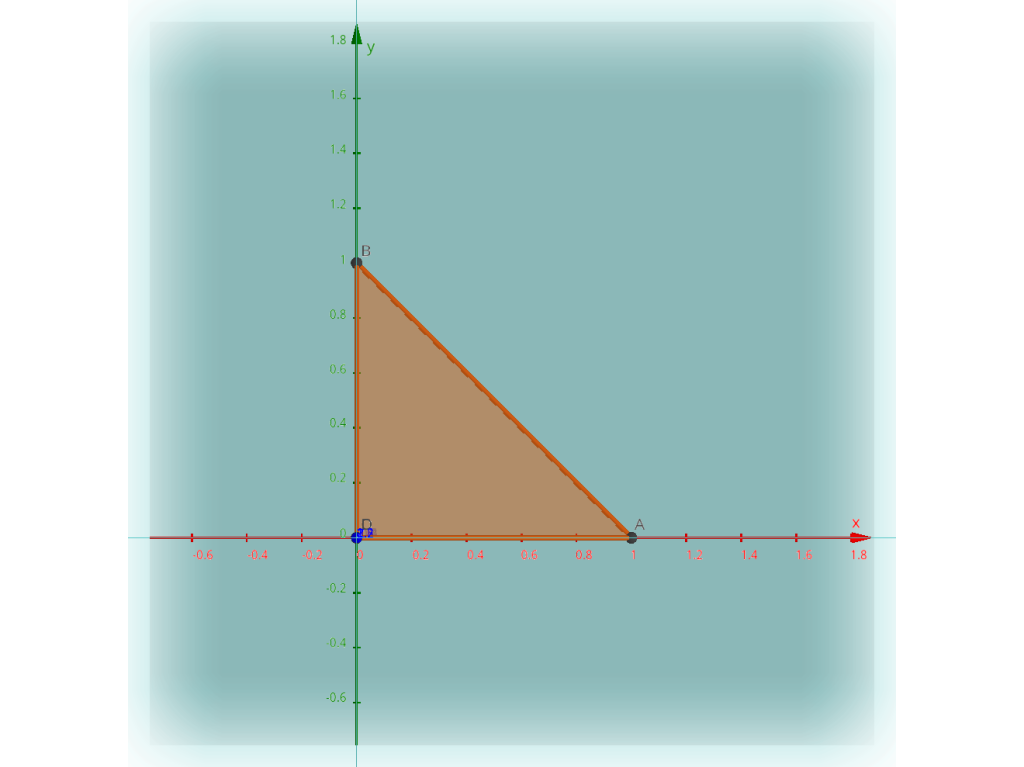
Но из этих частей ограниченная – только одна, и она представляет собой тетраэдр. Его грань, лежащая на плоскости $\left(x,y\right)$, изображена ниже:
Здесь $x$ лежит от 0 до 1, а $y$ лежит от 0 до $1-x$. Весь остальной тетраэдр лежит над этой гранью, и $z$ проходит от нуля до значения на верхней грани, т.е. на наклонной плоскости $1-x-y$: \[ \iiint\limits_{V}\frac{dxdydz}{\left(1+x+y+z\right)^{3}}=\int\limits_{0}^{1}dx\int\limits_{0}^{1-x}dy\int\limits_{0}^{1-x-y}dz\frac{1}{\left(1+x+y+z\right)^{3}} \] Считать будем изнутри наружу. Первый: \[ \int\limits_{0}^{1-x-y}dz\frac{1}{\left(1+x+y+z\right)^{3}}=-\frac{1}{2}\left.\frac{1}{\left(1+x+y+z\right)^{2}}\right|_{0}^{1-x-y}=-\frac{1}{2}\left(\frac{1}{\left(1+x+y+\left(1-x-y\right)\right)^{2}}-\frac{1}{\left(1+x+y\right)^{2}}\right)= \] \[ =-\frac{1}{2}\left(\frac{1}{4}-\frac{1}{\left(1+x+y\right)^{2}}\right) \] Второй: \[ \int\limits_{0}^{1-x}dy\int\limits_{0}^{1-x-y}dz\frac{1}{\left(1+x+y+z\right)^{3}}=-\frac{1}{2}\int\limits_{0}^{1-x}dy\left(\frac{1}{4}-\frac{1}{\left(1+x+y\right)^{2}}\right)=-\frac{1}{2}\left.\left(\frac{y}{4}+\frac{1}{1+x+y}\right)\right|_{0}^{1-x}= \] \[ =-\frac{1}{2}\left[\left(\frac{1-x}{4}+\frac{1}{1+x+1-x}\right)-\left(\frac{1}{1+x}\right)\right]=-\frac{1}{2}\left(\frac{3}{4}-\frac{x}{4}-\frac{1}{1+x}\right) \] Третий: \[ \iiint\limits_{V}\frac{dxdydz}{\left(1+x+y+z\right)^{3}}=\int\limits_{0}^{1}dx\int\limits_{0}^{1-x}dy\int\limits_{0}^{1-x-y}dz\frac{1}{\left(1+x+y+z\right)^{3}}=-\frac{1}{2}\int\limits_{0}^{1}dx\left(\frac{3}{4}-\frac{x}{4}-\frac{1}{1+x}\right)= \] \[ =-\frac{1}{2}\left.\left(\frac{3}{4}x-\frac{x^{2}}{8}-\ln\left|1+x\right|\right)\right|_{0}^{1}=-\frac{1}{2}\left(\frac{3}{4}-\frac{1}{8}-\ln2\right)=\frac{1}{2}\ln2-\frac{5}{16}. \]
Задание: № 4076, 4078, 4079.
Так же, как и в двойных, в тройных интегралах можно менять порядок интегрирования. Для этого понадобится заново расставлять пределы интегрирования, а для этого надо сначала построить область интегрирования по старым пределам.
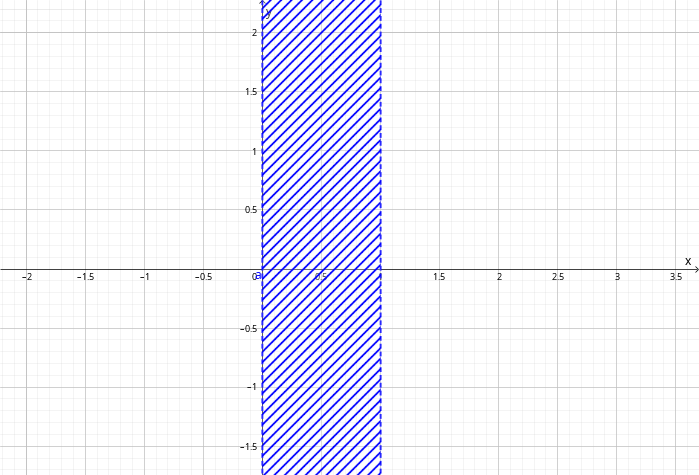
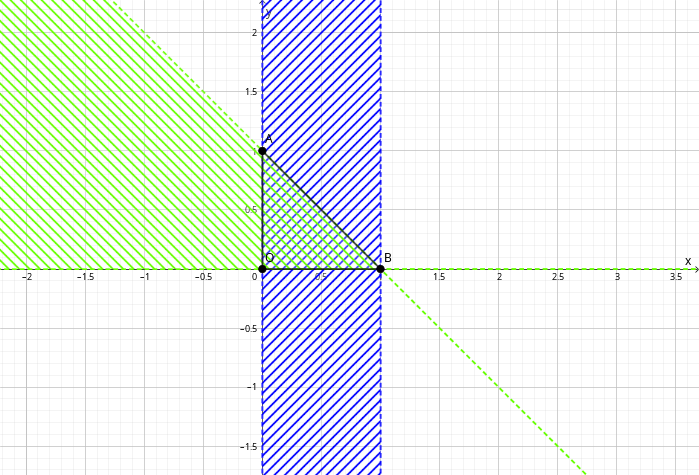
Пример: № 4081 Различными способами расставить пределы интеграции в интеграле \[ \int\limits_{0}^{1}dx\int\limits_{0}^{1-x}dy\int\limits_{0}^{x+y}f\left(x,y,z\right)dz. \] Вот в таких пределах меняются переменные: $0\leqslant x\leqslant1$, $0\leqslant y\leqslant1-x$, $0\leqslant z\leqslant x+y$. Начнём строить область, описываемую ими. Если $0\leqslant x\leqslant1$, то на плоскости $\left(x,y\right)$ так описывается вертикальная полоса:
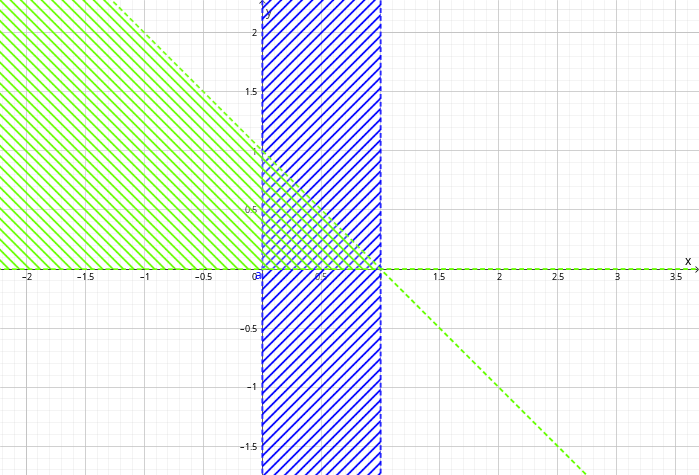
Далее строим прямые $y=0$ и $y=1-x$, и выделяем область, где $0\leqslant y\leqslant1-x$. Это будет угол:
К обеим областям принадлежит треугольник $\triangle AOB$:
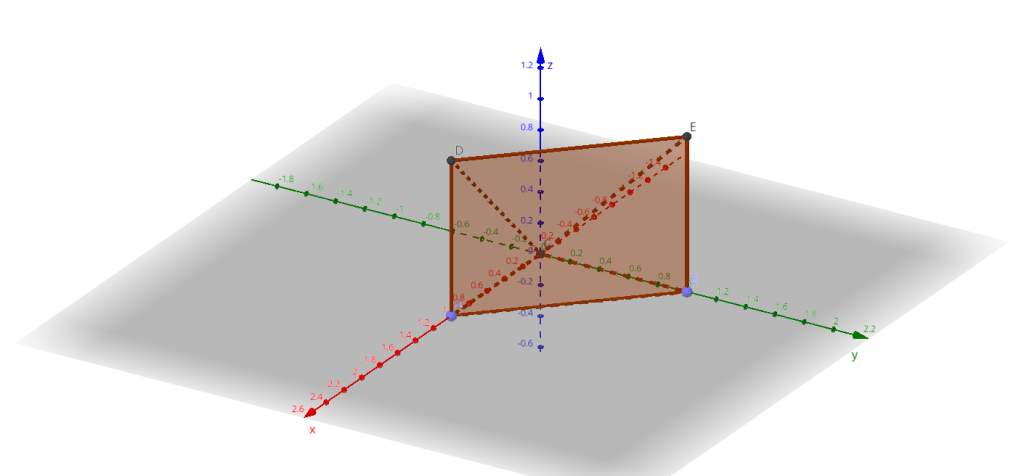
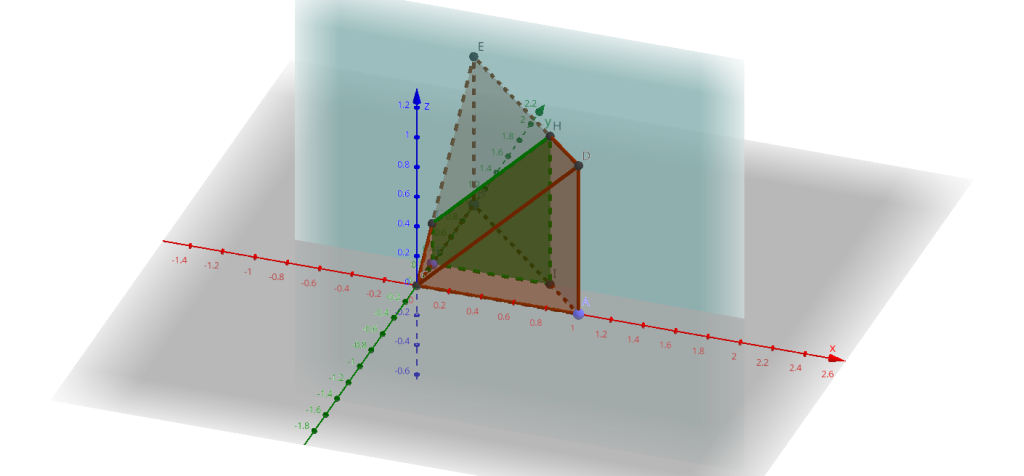
Разумеется, если добавить ось $z$, то треугольник превращается в трубу треугольного сечения, перпендикулярную плоскости чертежа. Сверху и снизу от этой трубы отсекается некая часть: плоскостью $z=0$, т.е. плоскостью $\left(x,y\right)$, и плоскостью $z=x+y$. Сечение треугольной трубы плоскостью $z=x+y$ представляет собой тоже треугольник, образованный пересечениями плоскости $z=x+y$ с рёбрами трубы: осью $z$ и двумя параллельными ей осями, проходящими через точки $A$ и $B$. На пересечении с осью $z$ $x=y=0$, $z=x+y=0+0=0$, и это пересечение произойдёт в начале координат. Над точками $A$ и $B$, имеющими координаты $\left(1,0\right)$ и $\left(0,1\right)$, $z=1$. Снизу труба закрывается уже построенным треугольником $\triangle AOB$, порождая замкнутое тело (это будет пирамида, лежащая на боку с вершиной в точке $O$):
Расставим интегралы в следующем порядке: снаружи пусть будет интеграл по $y$, который на всей пирамиде меняется от 0 до 1. Дальше пределы для остальных переменных расставляются для данного $y$. Точки пирамиды при данном $y$ образуют сечение пирамиды плоскостью $y=const$. Эта плоскость параллельна плоскости $y=0$ и пересекает плоскости $x=0$, $z=0$, $y=1-x$ и $z=x+y$:
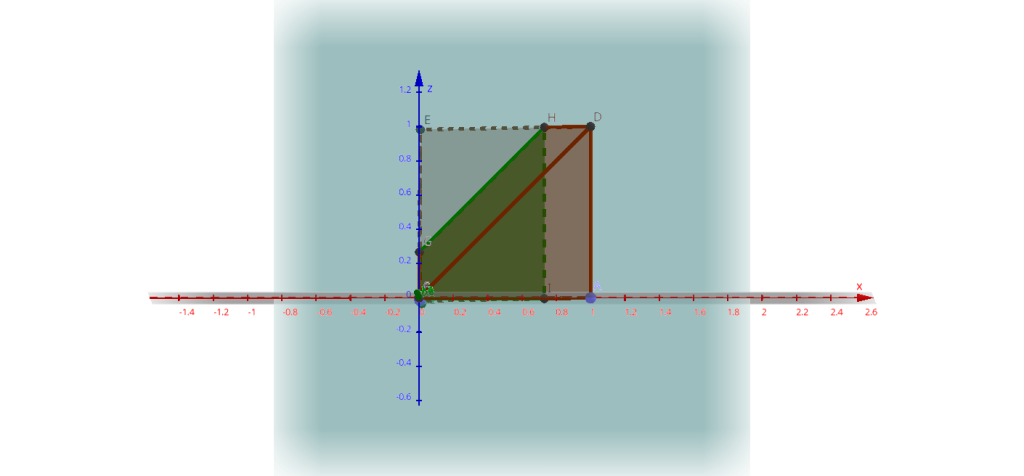
Сечение образует зелёную трапецию, которая при $y=0$ превращается в треугольную грань фигуры на плоскости $\left(x,z\right)$, а при $y=1$ вырождается в ребро $BE$:
На этой трапеции $x$ (если его интеграл ставить в середину) меняется от 0 до $y-1$, а $z$ – от 0 до $x+y$: \[ \int\limits_{0}^{1}dx\int\limits_{0}^{1-x}dy\int\limits_{0}^{x+y}f\left(x,y,z\right)dz=\int\limits_{0}^{1}dy\int\limits_{0}^{1-y}dx\int\limits_{0}^{x+y}f\left(x,y,z\right)dz. \]
Задание: расставить интегралы в № 4081 в порядке \[ \int\limits dz\int\limits dx\int\limits dyf\left(x,y,z\right). \]
Задание: № 4082