Доказать:
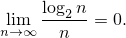
Пусть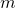 
– целая часть 
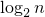. Тогда 
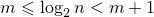. Это неравенство
также можно записать в видах 
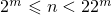и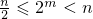 
. Так как 
,
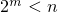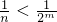. В сочетании с неравенством 
(
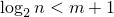и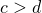 
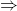
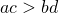) это даёт
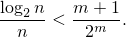 | (1) |
Легко вывести, например, из ранее полученного результата задачи №58, что
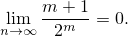
Это означает, что для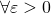 
существует 
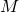, начиная с которого (т.е. при
) 
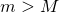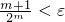. Возьмём теперь целое 
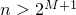. Тогда
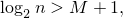
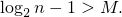
Но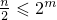 
, значит,
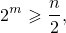
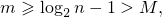
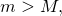
а при этом условии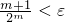 
. Но так как (1),
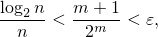
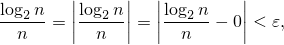
при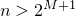 
, для 
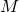, существующего для любого 
. Следовательно, по
определению предела, пределом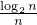 
является ноль.
Расширить данное доказательство на логарифм по основанию a предлагается самостоятельно.
