Если правая часть неоднородного уравнения, записанного в каноническом виде \begin{equation} \sum_{k=0}^{n}a_{k}y^{(k)}=f\left(x\right)\label{eq:main} \end{equation} не относится к одному из рассмотренных выше классов функций, можно воспользоваться методом вариации постоянных. Он более хлопотный, но может применяться в качестве оружия последнего шанса.
01.11.2021
08.05.2021
Задания и материалы для дистанционного занятия гр. 06-061 в 8:30 в пн. 3.05.2021 (Филиппов № 113, 114, 124)
Уравнения вида \begin{equation} y'=f\left(\frac{ax+by+c}{px+qy+r}\right)\label{eq:ob_odn} \end{equation}
03.05.2021
Задания и материалы для дистанционного занятия гр. 06-061 в 8:30 в пн. 3.05.2021 (Филиппов № 53, 62, 103)
Всякое уравнение, содержащее более одной переменной, связывает эти переменные. Даже когда мы задаём функцию вида $y=f\left(x\right)$, мы пишем уравнение. Это уравнение уже разрешено относительно переменной $y$, но его можно решить и относительно переменной $x$.
Дифференциальными называются уравнения, содержащие производные одной переменной по другой.
09.12.2020
О понижении порядка уравнений в системах на примере № 822
И последнее, что я должен сообщить про системы уравнений. Если уравнения в системе линейны, но имеют порядок выше первого, то можно добавлением новых функций от $t$ свести систему к системе первого порядка, но с бОльшим числом уравнений.
Да, такие задания могут попасться в контрольной работе.
31.05.2020
Задания и материалы для дистанционного занятия гр. 06-812 в вт 2.05.2020, 10:10 (Филиппов, №1170, 1175, 1196)
Образовалось одно неучтённое занятие, а так как формально у нас продолжается курс дифференциальных уравнений, хотелось бы показать ещё одну вещь, которая очень пригодится в следующем семестре на математической физике — уравнения в частных производных, хотя бы линейные и хотя бы первого порядка.
Рассмотрим линейное однородное уравнение в частных производных первого порядка в случае трёх независимых переменных: \begin{equation} Pu_{x}'+Qu_{y}'+Ru_{z}'=0,\label{or_odn} \end{equation} где $P,Q,R$ зависят от $x,y,z$.
18.11.2019
Филиппов №437 (для тов. Толмачёвой и других интересующихся)
Решить уравнение:
\[
y^{\prime\prime}=e^{y}
\]
(more…)
19.11.2016
Интеграл из №681 для гр. 06-512
Студенты из гр. 512 не смогли взять интеграл, нужный для нахождения $z$. Берётся он так:
(more…)
28.10.2015
Филиппов №681
Я задал группе 06-410 уравнения, решаемые методом Остроградского-Лиувилля, а примеров не показал. Показываю:
(more…)
16.10.2013
14.10.2013
Давно обещал
Тов. Ларин интересовался, как решается первое уравнение из третьего варианта
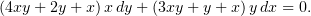
Решается оно так.

