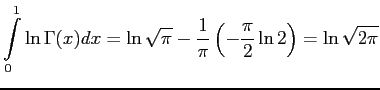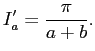Сначала возьмём вспомогательный интеграл:
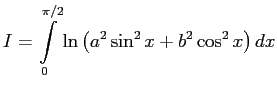 |
(1) |
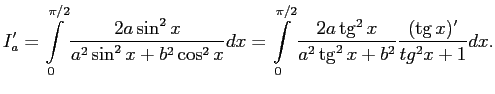
Заменяя
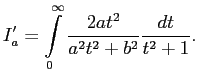
Опуская подробности взятия интеграла рациональной функции, обьявлю конечный результат:
Аналогично находится, что
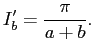
Отсюда
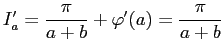
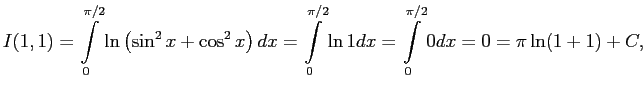
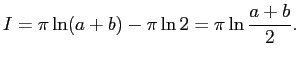
Вернёмся теперь к основному интегралу этого номера.
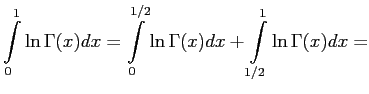
В первом из этих интегралов произведём замену вида
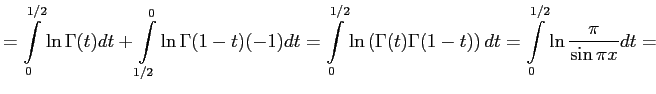
Заменим теперь
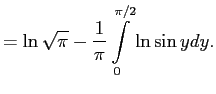
Последний интеграл возьмём, используя найдённую функцию
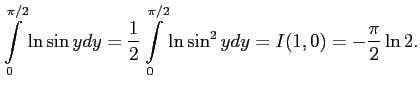
Тогда