Страница сетевой поддержки учеников Тимура Юрьевича Альпина

16.12.2009

Анчиков №105

Filed under: век. ан. — Shine @ 1:47 дп
Найти циркуляцию вектора $ \vec F=y^2\vec i+xy\vec j+(x^2+y^2)\vec k$ по контуру, вырезаемому в первом октанте из параболоида $ x^2+y^2=az$ плоскостями $ x=0$ , $ y=0$ , $ z=a$ ($ a>0$ ) в положительном направлении относительно внешней нормали параболоида.

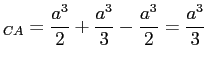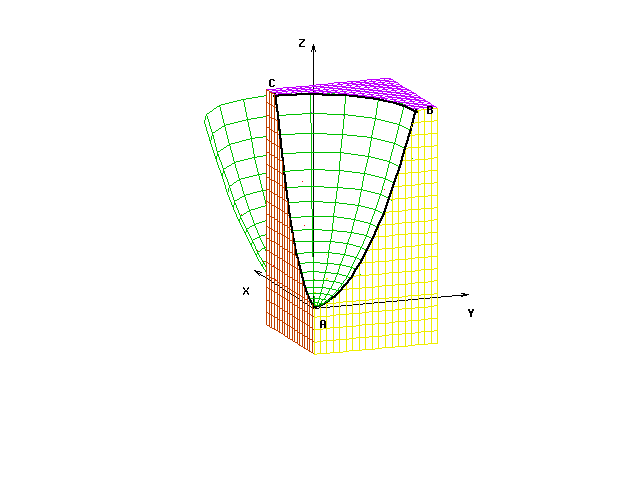
Контур вместе с поверхностями, которыми он образован, изображён на рисунке. Внешняя нормаль параболоида направлена к зрителю, следовательно, обход контура производится в последовательности $ A\rightarrow B \rightarrow C$ .

Найдём координаты точек $ A$ , $ B$ и $ C$ . Каждая из этих точек является точкой пересечения трёх поверхностей, и её координаты удовлетворяют трём уравнениям поверхностей. Точка $ A$ лежит на пересечении всех поверхностей, кроме $ z=a$ , значит, $ x=0$ , $ y=0$ ; $ az=0^2+0^2$ , $ z=0$ : $ A(0,0,0)$ . Точка $ B$ лежит на пересечении всех поверхностей, кроме $ y=0$ , значит, $ x=0$ , $ z=a$ ; $ y^2=az=a^2$ , $ y=\pm a$ . Т.к. рассматривается первый октант, оставляем вариант $ y=a$ : $ B(0,a,a)$ . Точка $ C$ лежит на пересечении всех поверхностей, кроме $ x=0$ , значит, $ y=0$ , $ z=a$ ; $ x^2=az=a^2$ , $ x=\pm a$ . Т.к. рассматривается первый октант, оставляем вариант $ x=a$ : $ C(a,0,a)$ .

Искомая циркуляция равна

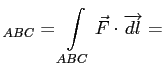   Ц$\displaystyle _{ABC}=\int\limits_{ABC} \vec F \cdot \overrightarrow{dl}=$Ц$\displaystyle _{AB}+$Ц$\displaystyle _{BC}+$Ц$\displaystyle _{CA} $

Сосчитаем слагаемые в последнем разложении по отдельности.

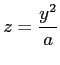AB) $ x=0$ , $ z=\dfrac{y^2}{a}$ , $ 0\leqslant y\leqslant a$ .

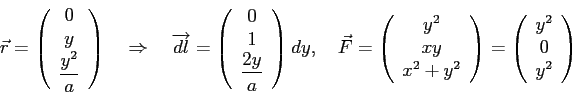
\begin{displaymath} \vec r=\left( \begin{array}{c} 0 \\ y \\ \dfrac{y^2}{a} \en... ...)= \left( \begin{array}{c} y^2 \\ 0 \\ y^2 \end{array}\right) \end{displaymath}

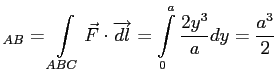
   Ц$\displaystyle _{AB}=\int\limits_{ABC} \vec F \cdot \overrightarrow{dl}=\int\limits_0^a \frac{2y^3}{a}dy=\frac{a^3}{2} $

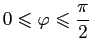BC) $ z=a$ , $ x^2+y^2=a^2$ . При прохождении параметром промежутка, точка с координатами-функциями этого параметра должна переместиться по дуге окружности $ z=a$ , $ x^2+y^2=a^2$ из точки $ B$ в точку $ C$ . Нетрудно проверить, что этим условиям удовлетворяет параметризация $ y=a\cos \varphi$ , $ x=a\sin \varphi$ , $ 0\leqslant \varphi \leqslant \dfrac{\pi}{2}$ .

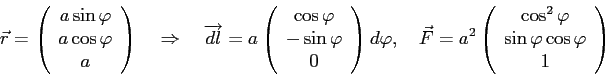
\begin{displaymath} \vec r=\left( \begin{array}{c} a\sin \varphi \\ a\cos \varp... ...cos^2\varphi \\ \sin\varphi\cos\varphi \\ 1 \end{array}\right) \end{displaymath}

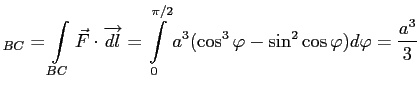
   Ц$\displaystyle _{BC}=\int\limits_{BC}\vec F\cdot \overrightarrow{dl}= \int\limits_0^{\pi/2}a^3(\cos^3\varphi-\sin^2\cos \varphi)d\varphi=\frac{a^3}{3} $

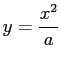CA) $ y=0$ , $ y=\dfrac{x^2}{a}$ , $ x=a(1-t)$ , $ 0\leqslant t\leqslant 1$

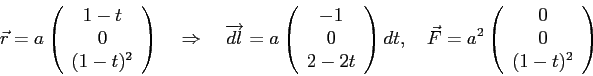
\begin{displaymath} \vec r=a\left( \begin{array}{c} 1-t \\ 0 \\ (1-t)^2 \end{ar... ...2\left( \begin{array}{c} 0 \\ 0 \\ (1-t)^2 \end{array}\right) \end{displaymath}

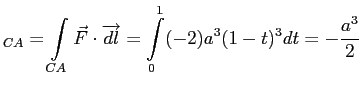
   Ц$\displaystyle _{CA}=\int\limits_{CA}\vec F\cdot \overrightarrow{dl}= \int\limits_0^1 (-2)a^3(1-t)^3 dt=-\frac{a^3}{2} $

Наконец,

   Ц$\displaystyle =$Ц$\displaystyle _{AB}+$Ц$\displaystyle _{BC}+$Ц$\displaystyle _{CA}= \frac{a^3}{2}+\frac{a^3}{3}-\frac{a^3}{2}=\frac{a^3}{3} $

Комментариев нет »

No comments yet.

RSS feed for comments on this post.

Leave a comment

Для отправки комментария вам необходимо авторизоваться.

Хостингом угостил Вадим "Moose" Калинников