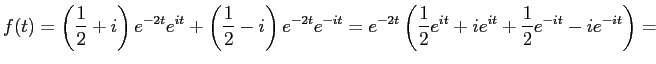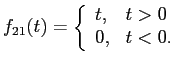Более развёрнутое решение, чем в методичке. Особенно рекомендуется тем, кто не понял решение оттуда.
Найти оригинал функции
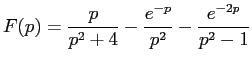
Эта функция является линейной комбинацией трёх функций, следовательно её оригинал - это линейная комбинация с теми же коэффициентами их оригиналов. Найдём их по очереди, слева направо.
- Выражение
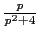 напоминает нам правую часть равенства
напоминает нам правую часть равенства
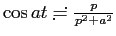 , при
, при 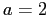 имеем
имеем
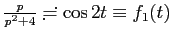 .
.
-
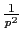 соответствует функции
соответствует функции
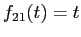 . Если быть точным - функции такой:
. Если быть точным - функции такой:
По теореме запаздывания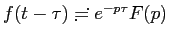 . Следовательно, для того, чтобы получить в образе множитель
. Следовательно, для того, чтобы получить в образе множитель 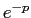 , надо от аргумента функции
, надо от аргумента функции 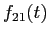 вычесть 1. При этом получится функция
вычесть 1. При этом получится функция
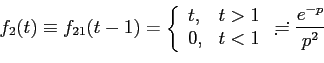
Отклоняясь от темы, отмечу, что в этом месте возникают затруднения у тех, кто не видит разницы между функциями, при помощи которых обозначаются оригиналы, и самими функциями-оригиналами. Конструкции типа (1) громоздки, поэтому в математических текстах выписывается только та их часть, которая "включается" при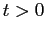 . И если сначала вычесть из
. И если сначала вычесть из 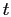 1, а потом составить оригинал
1, а потом составить оригинал
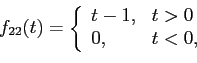
а потом найти его изображение - получится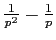 , а не то, что надо.
, а не то, что надо.
-
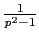 намекает на
намекает на 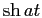 при
при 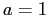 . Осталось вычесть из аргумента 2, чтобы организовать множитель
. Осталось вычесть из аргумента 2, чтобы организовать множитель 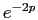 :
:
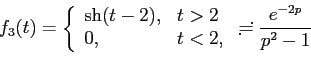
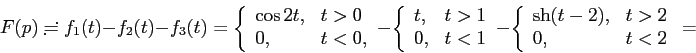
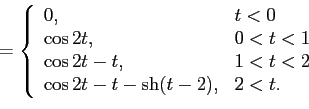
Задача 9.30 Найти оригинал функции
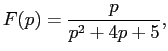
воспользовавшись второй теоремой разложения.
Вторая теорема разложения гласит, что
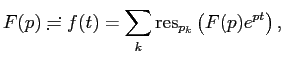
где
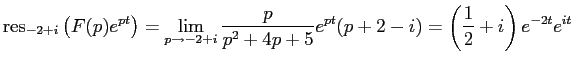
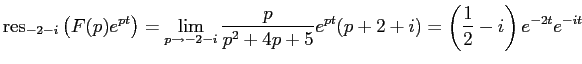
Теперь найдём