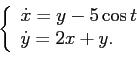
Систему эту можно представить в виде
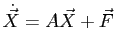 , где
, где
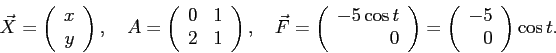
Исследование матрицы
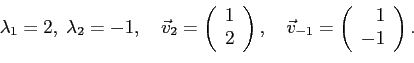
Следовательно, столбец
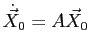 , запишется так:
, запишется так:
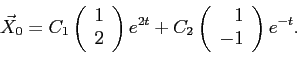
![\begin{displaymath}
\vec F=
\left[
\left(
\begin{array}{r}
P_m^{1}(t) \\
P_m^{2...
...Q_m^{2}(t)
\end{array}\right)\sin \beta t
\right]e^{\alpha t},
\end{displaymath}](http://shine.ylsoftware.com/math-img/fil827/img10.png)
где
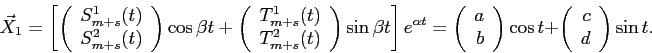
Подставляя такой
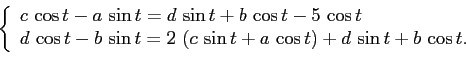
При
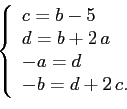
Решая эту систему, получим:
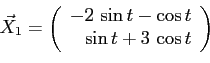
Для записи ответа учтём, что
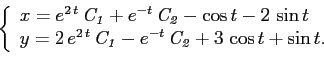
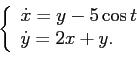
Систему эту можно представить в виде
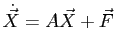 , где
, где
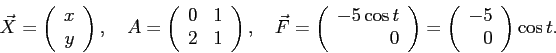
Исследование матрицы
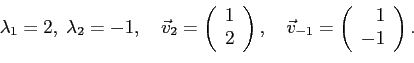
Следовательно, столбец
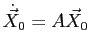 , запишется так:
, запишется так:
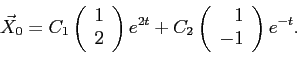
![\begin{displaymath}
\vec F=
\left[
\left(
\begin{array}{r}
P_m^{1}(t) \\
P_m^{2...
...Q_m^{2}(t)
\end{array}\right)\sin \beta t
\right]e^{\alpha t},
\end{displaymath}](http://shine.ylsoftware.com/math-img/fil827/img10.png)
где
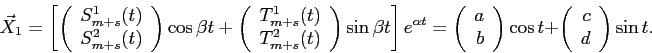
Подставляя такой
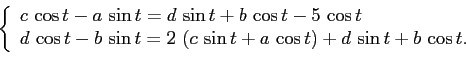
При
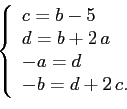
Решая эту систему, получим:
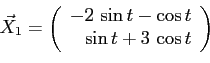
Для записи ответа учтём, что
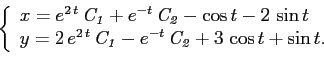
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников