Страница сетевой поддержки учеников Тимура Юрьевича Альпина

04.11.2010

Филиппов №754

Filed under: диф. уравнения — Shine @ 6:12 пп
Решить уравнение

$\displaystyle y''+y=1$

с граничными условиями

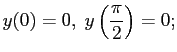
$\displaystyle y(0)=0,\; y\left(\frac{\pi}{2}\right)=0; $

используя функцию Грина.

В начале решим однородное уравнение $ y''+y=0$ , для чего составим характеристическое уравнение $ \lambda^2+1=0$ . Из последнего получим $ \lambda=\pm i$ . Решение, соответствующее этой паре корней $ y_0=C_1\cos x+C_2\sin x$ . Используя это решение, составим функцию Грина:

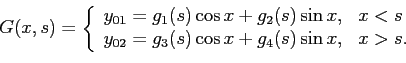
\begin{displaymath} G(x,s)=\left\lbrace \begin{array}{ll} y_{01}=g_1(s)\cos x+g_... ...\ y_{02}=g_3(s)\cos x+g_4(s)\sin x, & x>s. \end{array}\right. \end{displaymath}

Найдя функцию Грина, найдём искомую функцию $ y(x)$ по формуле

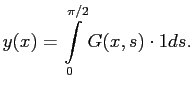
$\displaystyle y(x)=\int\limits_0^{\pi/2} G(x,s)\cdot 1 ds. $

Учтём граничные условия:

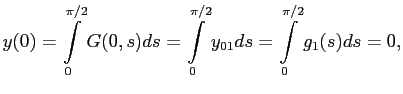
$\displaystyle y(0)=\int\limits_0^{\pi/2} G(0,s) ds=\int\limits_0^{\pi/2} y_{01} ds=\int\limits_0^{\pi/2} g_1(s) ds=0, $

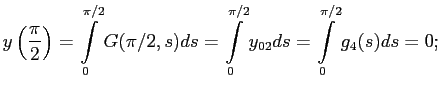
$\displaystyle y\left(\frac{\pi}{2}\right)=\int\limits_0^{\pi/2} G(\pi/2,s) ds=\int\limits_0^{\pi/2} y_{02} ds=\int\limits_0^{\pi/2} g_4(s) ds=0; $

которые удовлетворяются при $ g_1(s)=g_4(s)=0$ . Теперь используем условия сшивки $ y_{01}$ и $ y_{02}$ :

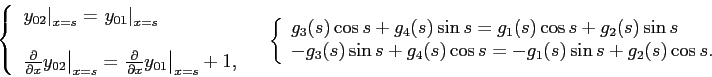
\begin{displaymath} \left\lbrace \begin{array}{l} \left. y_{02}\right\vert _{x=s... ... s+g_4(s)\cos s=-g_1(s)\sin s+g_2(s)\cos s. \end{array}\right. \end{displaymath}

Решая систему

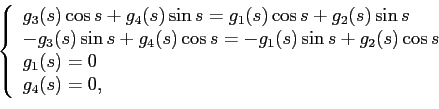
\begin{displaymath} \left\lbrace \begin{array}{l} g_3(s)\cos s+g_4(s)\sin s=g_1(... ...n s+g_2(s)\cos s \\ g_1(s)=0 \\ g_4(s)=0, \end{array}\right. \end{displaymath}

получим: $ g_1(s)=0,g_2(s)=-\cos s,g_3(s)=-\sin s,g_4(s)=0$ . Подставив найденные функции $ g_k(s)$ в функцию Грина, а функцию Грина - в формулу для $ y(x)$ , вычислим:

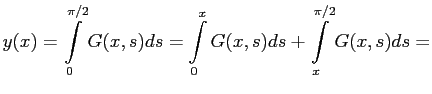
$\displaystyle y(x)=\int\limits_0^{\pi/2} G(x,s) ds=\int\limits_0^{x} G(x,s) ds+\int\limits_x^{\pi/2} G(x,s) ds= $

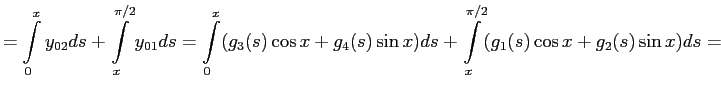
$\displaystyle =\int\limits_0^{x} y_{02} ds+\int\limits_x^{\pi/2} y_{01} ds= \in... ...)\cos x+g_4(s)\sin x) ds+\int\limits_x^{\pi/2} (g_1(s)\cos x+g_2(s)\sin x) ds= $

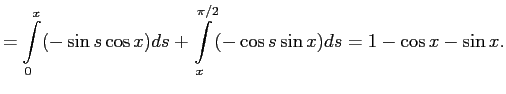
$\displaystyle =\int\limits_0^{x} (-\sin s\cos x) ds+\int\limits_x^{\pi/2} (-\cos s\sin x) ds= 1-\cos x -\sin x. $

Итак, $ y(x)=1-\cos x -\sin x$ . Идентичный результат можно получить, решив исходное уравнение обычными методами и найдя постоянные параметры из граничных условий.

Комментариев нет »

No comments yet.

RSS feed for comments on this post.

Leave a comment

Для отправки комментария вам необходимо авторизоваться.

Хостингом угостил Вадим "Moose" Калинников