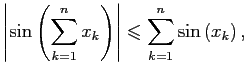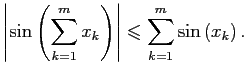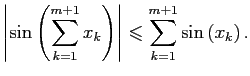Привет, МГИМО — 2 « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

20.02.2011

Привет, МГИМО — 2

Filed under: внешнее — Shine @ 7:24 пп

Доказать, что

$\displaystyle \left\vert\sin\left( \sum\limits_{k=1}^{n}x_k \right) \right\vert\leqslant \sum\limits_{k=1}^{n} \sin\left(x_k \right),$

(1)

где $0\leqslant x_k\leqslant \pi$ .

Докажем базу. Пусть $n=1$ . Тогда неравенство (1) превращается в $\vert\sin x_k\vert \leqslant \sin x_k$ , что при $0\leqslant x_1\leqslant \pi$ , безусловно, верно.

Теперь докажем шаг индукции. Пусть неравенство (1) верно при $n=m$ . Докажем его для $n=m+1$ .

Нам известно, что

$\displaystyle \left\vert\sin\left( \sum\limits_{k=1}^{m}x_k \right) \right\vert\leqslant \sum\limits_{k=1}^{m} \sin\left(x_k \right).$

(2)

Отсюда надо доказать, что

$\displaystyle \left\vert\sin\left( \sum\limits_{k=1}^{m+1}x_k \right) \right\vert\leqslant \sum\limits_{k=1}^{m+1} \sin\left(x_k \right).$

(3)

Рассмотрим левую часть неравенства (3). Из свойств тригонометрических функций получим:

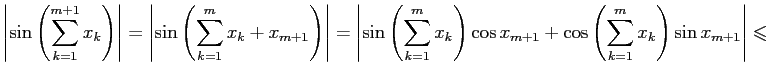
$\displaystyle \left\vert\sin\left( \sum\limits_{k=1}^{m+1}x_k \right) \right\ve... ...+ \cos\left( \sum\limits_{k=1}^{m}x_k \right)\sin x_{m+1}\right\vert\leqslant$

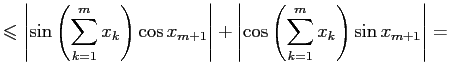
$\displaystyle \leqslant \left\vert\sin\left( \sum\limits_{k=1}^{m}x_k \right)\... ... \left\vert\cos\left( \sum\limits_{k=1}^{m}x_k \right)\sin x_{m+1}\right\vert=$

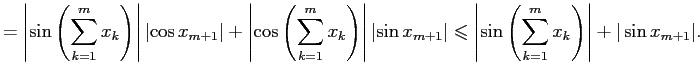
$\displaystyle =\left\vert\sin\left( \sum\limits_{k=1}^{m}x_k \right)\right\vert... ...sin\left( \sum\limits_{k=1}^{m}x_k \right)\right\vert+ \vert\sin x_{m+1}\vert.$

При последнем шаге мы воспользовались тем, что $\vert\cos \alpha\vert\leqslant 1$ . Прибавив к неравенству (2) $\vert\sin x_{m+1}\vert$ и учтя, что при $0\leqslant x_{m+1}\leqslant \pi$ будет $\sin x_{m+1}\geqslant 0$ и, следовательно, $\vert\sin x_{m+1}\vert=\sin x_{m+1}$ , получим:

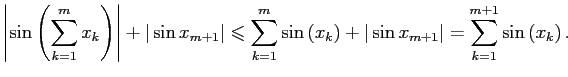
$\displaystyle \left\vert\sin\left( \sum\limits_{k=1}^{m}x_k \right) \right\vert... ...\right)+\vert\sin x_{m+1}\vert= \sum\limits_{k=1}^{m+1} \sin\left(x_k \right).$

Таким образом,

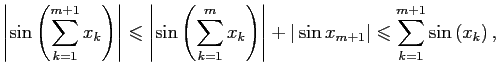
$\displaystyle \left\vert\sin\left( \sum\limits_{k=1}^{m+1}x_k \right) \right\ve... ...\vert\sin x_{m+1}\vert\leqslant \sum\limits_{k=1}^{m+1} \sin\left(x_k \right),$