3470
Преобразовать уравнение
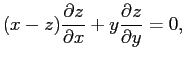
приняв
за функцию, а 
и 
- за независимые переменные.
Чтобы сразу избежать путаницы, введём новые обозначения для переменных в уравнении после замены: пусть 
и 
- новые независимые переменные, а 
- новая функция.
Продифференцируем перечисленные уравнения замены по
и
:
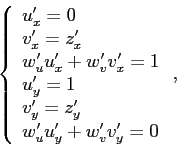
решим их относительно
и 
:
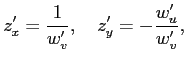
и подставим в исходное уравнение, умножив его на
:
Теперь полученное уравнение умножим на -1 и заменим обратно новые переменные на старые:
3471
Преобразовать уравнение
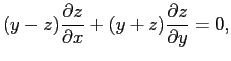
приняв
за функцию, а 
и 
- за независимые переменные.
Пусть новая функция в процессе решения обозначается
. Продифференцируем перечисленные уравнения замены по
и
:
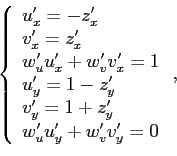
решим их относительно
и
:
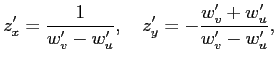
и подставим в исходное уравнение, умножив его на
:
Заменяя старые переменные
и
на новые, получим:
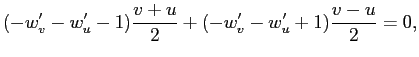
что при упрощении и замене временного обозначения
обратно на
даст
