Исследовать сходимость ряда:
Представим данный ряд в виде
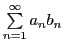
,
где
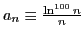
,
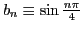
и докажем, что он сходится по признаку Дирихле. Обозначим частичные суммы второй последовательности так:
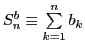
.
Заметим, что они периодичны. Во-первых,
Во-вторых, (во второй суме преобразуем
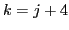
)
Осталось доказать, что
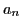
монотонно стремится к нулю. Для этого рассмотрим две функции:
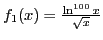
и
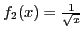
. При
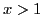
явно
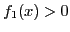
. С другой стороны существует такое
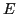
, что при
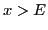
функция
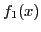
убывает. Докажем это:
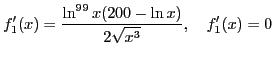
при
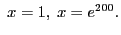
При
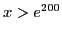
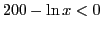
, все же остальные множители
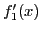
положительны. Значит,
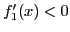
, следовательно,
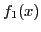
- убывающая функция при
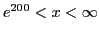
. Так как она убывает и ограничена снизу нулём, она является ограниченной функцией. на этом же интервале явно убывает и стремится к нулю. Следовательно,
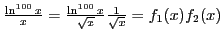
, как произведение убывающих функций - монотонно убывает, а как произведение ограниченной функции на стремящуюся к нулю - стремится к нулю. Те же свойства наследует и аналогичная функция натурального аргумента: при
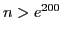
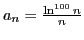
убывает и стремится к нулю.
Вследствие доказанных свойств последовательностей
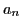
и
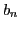
ряд
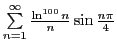
условно сходится по признаку Дирихле, что и требовалось доказать.
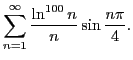
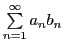 ,
где
,
где
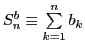 .
.
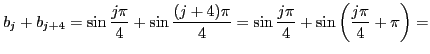
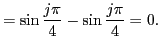
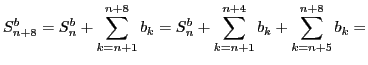
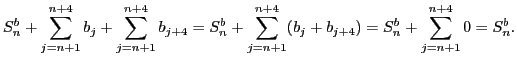
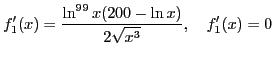 при
при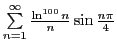 условно сходится по признаку Дирихле, что и требовалось доказать.
условно сходится по признаку Дирихле, что и требовалось доказать.
