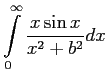Вычислить интеграл
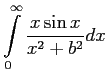 |
(1) |
(предполагается, что
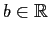
).
Рассмотрим вспомогательную функцию
При

модуль этой функции
Таким образом, с одной стороны,

, где второе выражение не зависит от

, с другой стороны,

. Следовательно, функция

стремится к нулю равномерно по

при

по признаку Вейерштрасса. Значит,
где

- особые точки функции

в верхней полуплоскости.
Функция

имеет особые точки

и

, причём только одна из них лежит в верхней полуплоскости. Заметим, что

входит в интеграл (
1) и функцию

только в виде

, следовательно, интеграл (
1) не может зависеть от знака

. Считая для определённости

, получим, что в верхней полуплоскости лежит точка

. Вычислим интеграл
Аналогично,
Тогда
Так как

есть функция чётная, окончательно вычислим интеграл (
1)



 , где второе выражение не зависит от
, где второе выражение не зависит от  . Следовательно, функция
. Следовательно, функция ![$\displaystyle \int\limits_{-\infty}^{\infty}e^{iax}f(x)dx
=
2\pi i\sum\limits_{k}\mathrm{res}_{z_k}\left[ f(z)e^{iaz}\right],
$](http://shine.ylsoftware.com/math-img/dk8-32/p_img12.png)
![$\displaystyle \int\limits_{-\infty}^{\infty}e^{ix}f(x)dx=2\pi i\,\mathrm{res}_{ib}\left[ f(z)e^{iz}\right]=\pi i e^{-b}.
$](http://shine.ylsoftware.com/math-img/dk8-32/p_img19.png)
![$\displaystyle \int\limits_{-\infty}^{\infty}e^{-ix}f(x)dx=2\pi i\,\mathrm{res}_{ib}\left[ f(z)e^{-iz}\right]=\pi i e^b.
$](http://shine.ylsoftware.com/math-img/dk8-32/p_img20.png)


 есть функция чётная, окончательно вычислим интеграл (1)
есть функция чётная, окончательно вычислим интеграл (1)