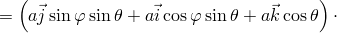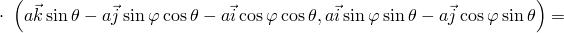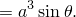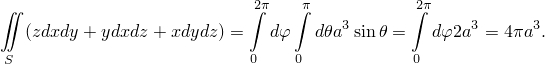Вычислить поверхностный интеграл второго рода:
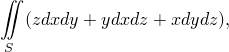 | (1) |
где 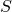 – внешняя сторона сферы
– внешняя сторона сферы 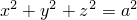 .
.
В сферических координатах уравнение поверхности запишется как 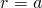 , следовательно, декартовы координаты
точек поверхности
, следовательно, декартовы координаты
точек поверхности
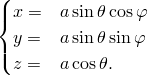 | (2) |
Для того, чтобы взять интеграл (1), его необходимо преобразовать к нижеследующему виду:
![∬ ∬ -→-→ 2∫π ∫π -→ [ ]
(zdxdy+ ydxdz + xdydz) = Fds = dφ dθF ⋅ -→r ′θ × -→r ′φ ,
S S 0 0](http://shine.ylsoftware.com/math-img/dem4362/dem43625x.png) | (3) |
где 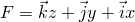 . Учитывая (2), вычислим подынтегральное выражение:
. Учитывая (2), вычислим подынтегральное выражение:
![-→F ⋅[-→r ′× -→r ′] =
θ φ](http://shine.ylsoftware.com/math-img/dem4362/dem43627x.png)
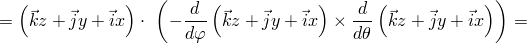
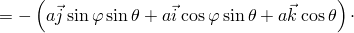
![[ ]
-d-( ⃗ ⃗ ⃗ ) d-( ⃗ ⃗ ⃗ )
⋅ dφ ajsinφ sinθ + aicosφ sin θ+ akcosθ × dθ aj sinφ sin θ+ aicosφsinθ+ ak cosθ =](http://shine.ylsoftware.com/math-img/dem4362/dem436210x.png)