Вычислить поверхностный интеграл второго рода
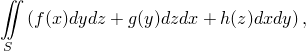
где 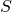 – внешняя сторона поверхности параллелепипеда
– внешняя сторона поверхности параллелепипеда  ;
; 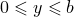 ;
;
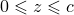 .
.
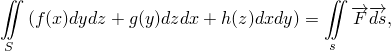
где 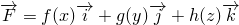 . С поверхностью сложнее. Общее правило
гласит, что интеграл по множеству равен сумме интегралов по подмножествам,
если эти подмножества не пересекаются, а их объединение образует исходное
множество. Для поверхностных интегралов второго рода оно тоже действует, и
интеграл по поверхности параллелепипеда есть сумма следующих интегралов: по
ближней грани, по дальней грани, по левой и правой граням, а также по верхней
и нижней граням. На каждой грани выбирается своя параметризация
поверхности.
. С поверхностью сложнее. Общее правило
гласит, что интеграл по множеству равен сумме интегралов по подмножествам,
если эти подмножества не пересекаются, а их объединение образует исходное
множество. Для поверхностных интегралов второго рода оно тоже действует, и
интеграл по поверхности параллелепипеда есть сумма следующих интегралов: по
ближней грани, по дальней грани, по левой и правой граням, а также по верхней
и нижней граням. На каждой грани выбирается своя параметризация
поверхности.
В частности, если ось  направлена на нас, ось
направлена на нас, ось  – вправо, а ось
– вправо, а ось  – вверх,
то ближняя грань задаётся уравнением
– вверх,
то ближняя грань задаётся уравнением 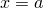 , радиус-вектор точек этой грани
, радиус-вектор точек этой грани
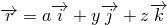 будет зависеть от параметров
будет зависеть от параметров 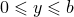 и
и 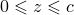 . Тогда
. Тогда
![−→ [−→ ′ −→ ′] d ( ) d ( )
ds = ry × r z dydz = dy ⃗kz + ⃗jy+ a⃗i × dz ⃗kz +⃗jy+ a⃗i dydz = ⃗j × ⃗k dydz = ⃗i dydz](http://shine.ylsoftware.com/math-img/dem4363/dem436314x.png) Вектор
Вектор 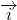 , имеющий то же направление, что и вектор
, имеющий то же направление, что и вектор 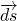 , на ближней грани
направлен из параллелепипеда, нам же требуется найти интеграл по внешней
стороне, следовательно направление
, на ближней грани
направлен из параллелепипеда, нам же требуется найти интеграл по внешней
стороне, следовательно направление 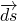 выбрано правильно. Тогда на ближней
грани
выбрано правильно. Тогда на ближней
грани 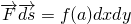 , и
, и
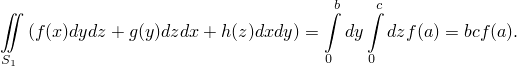
Аналогично для дальней стенки ![−→ds = [−→r ′z × −→r ′y]dydz = −⃗i dydz](http://shine.ylsoftware.com/math-img/dem4363/dem436320x.png) . Вектор
. Вектор
 будет сонаправлен вектору
будет сонаправлен вектору  , направленному вовне параллелепипеда для
дальней грани, значит
, направленному вовне параллелепипеда для
дальней грани, значит
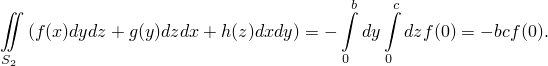
Сумма интегралов по ближней и дальней граням
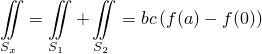
Точно так же для левой и правой стенок находится, что
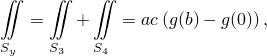
а для верхней и нижней - что
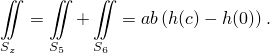
Следовательно,
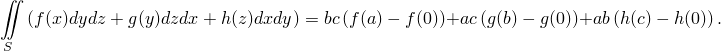

Так тут же, как говорит тов. Исхаков, ушеслышно все. Делаешь все по определению — получаешь нужный результат. 4360 посложнее
Комментарий by thx1138 — 09.11.2011 @ 2:56 пп