Страница сетевой поддержки учеников Тимура Юрьевича Альпина

Всё-таки придётся там заменять производную х.

Пропишем зависимости:

(%i1)

depends([x,y,z],t);

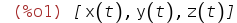
Чтобы производные обозначались в программе коротко, а не как dx/dt:

(%i2)

derivabbrev:true;

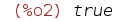
Система

(%i3)

eqns:[ diff(x,t,2)+diff(x,t)+diff(y,t)-2*y=0, diff(x,t)-diff(y,t)+x=0];

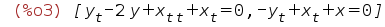
Обозначим список функций для дальнейшей автоматизации

(%i4)

X:[x,y,z];

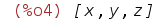
и объявим, как мы ввели z:

(%i5)

dop:diff(x,t)=z;

Теперь начнём решать. Заменим производные в системе

(%i6)

eqns,dop,diff(dop,t);

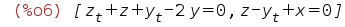
дополним систему объявлением z и выразим производные явно

(%i7)

append(%,[dop]);

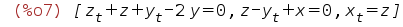
(%i8)

diff(X,t);

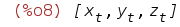
(%i9)

eqns2:solve(%th(2),%);

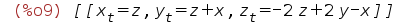
Сгенерируем матрицу А

(%i10)

%th(2),eqns2;

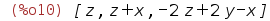
(%i11)

makelist(ev(%,X[i]=1),i,1,3);

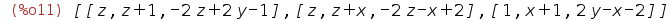
(%i12)

%,makelist(X[i]=0,i,1,3);

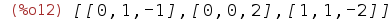
(%i13)

apply(matrix,%);

(%i14)

A:transpose(%);

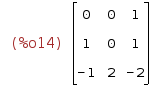
и найдём её собственные значения и векторы. В первом списке - список соб. значений и их кратностей, во втором -
собственных векторов.

(%i15)

eigA:eigenvectors(A);

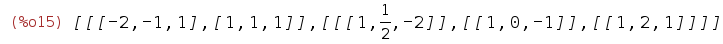
Ответ:

(%i16)

sum(C[i]*eigA[2][i][1]*exp(eigA[1][1][i]*t),i,1,3)-X;

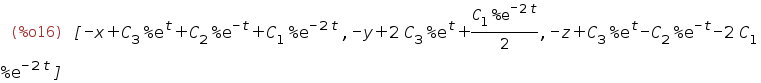
(%i17)

solve(%,X);

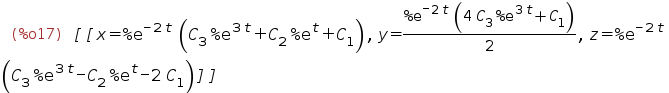
(%i18)

otvet:expand(%);

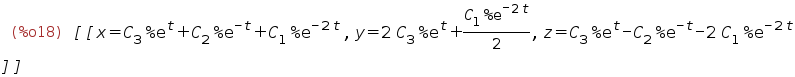
Проверка:

(%i19)

ev(eqns,otvet);

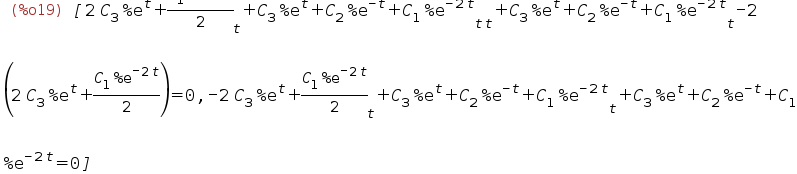
(%i20)

%,diff;

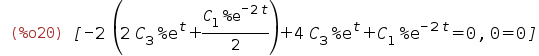
(%i21)

radcan(%);

---

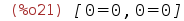
Created with wxMaxima.