Найти предел
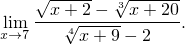
Заметим, что
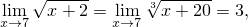
и добавим и вычтем в числителе 3:
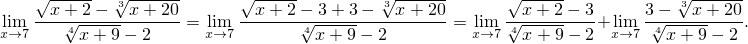 | (1) |
Сначала вычислим предел, который понадобится потом неоднократно:

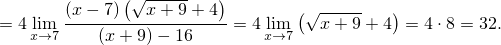
Теперь вычислим отдельно пределы из формулы (1):
Осталось сложить результаты:
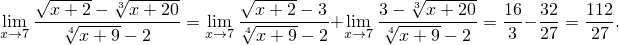
Найти предел
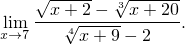
Заметим, что
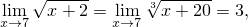
и добавим и вычтем в числителе 3:
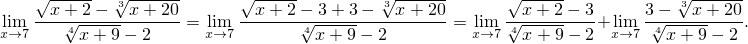 | (1) |
Сначала вычислим предел, который понадобится потом неоднократно:

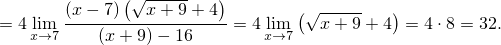
Теперь вычислим отдельно пределы из формулы (1):
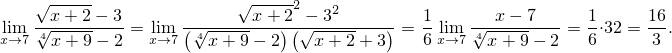
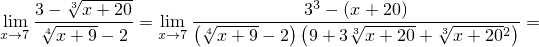
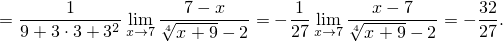
Осталось сложить результаты:
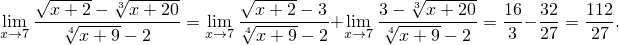
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников