Метод вариации постоянных и разное « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

03.10.2012

Метод вариации постоянных и разное

Filed under: диф. уравнения,пепел — Shine @ 3:22 пп

Что-то занесло меня сегодня.
Во-первых: в №551 коэффициенты неоднородного решения такие:
a=-5/8,~b=0,~c=0, d=5/16 .
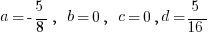Во-вторых, в конце занятия я пытался, но не смог объяснить следующее:

Рассмотрим линейное неоднородное уравнение порядка n:

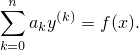∑n (k) aky = f(x). k=0

(1)

Пусть y_0m^(k) – решения однородного уравнения, т.е.

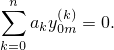∑n aky(k0m)= 0. k=0

(2)

Общее решение однородного уравнения будет иметь вид

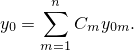
n y = ∑ C y . 0 m=1 m 0m

Рассмотрим функцию

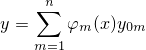∑n y = φm (x )y0m m=1

(3)

и попытаемся найти такие функции φ_m(x), чтобы y была решением уравнения (1).

Подберём φ_m(x) так, чтобы

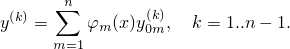n (k) ∑ (k) y = m=1φm (x)y0m, k = 1..n - 1.

(4)

В частности,

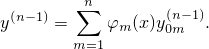
(n-1) ∑n (n-1) y = φm (x)y0m . m=1

Тогда по правилу Лейбница

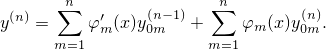(n) ∑n ′ (n- 1) ∑n (n) y = φm(x)y0m + φm (x )y0m. m=1 m=1

(5)

Подставим y такое в исходное уравнение (1). Отсоединим от суммы в левой части одно слагаемое и заменим производные по формулам (4) и (5):

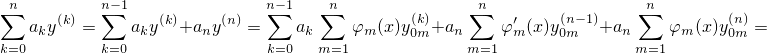
∑n n-∑ 1 n∑-1 ∑n ∑n n∑ aky(k) = aky(k)+any(n) = ak φm (x)y(0km)+an φ′m (x)y(0nm-1)+an φm (x)y(0nm)= k=0 k=0 k=0 m=1 m=1 m=1

Заметим, что первую и последнюю суммы можно объединить. После этого переставим слагаемые и множители:

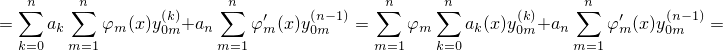
∑n ∑n ∑n ∑n ∑n ∑n = ak φm(x)y(0k)m+an φ′m(x)y(n0-m 1) = φm ak(x)y(k0m)+an φ ′m(x)y(n0m-1)= k=0 m=1 m=1 m=1 k=0 m=1

Далее заметим, что в первой сумме собралась сумма из (2). Вследствие этого

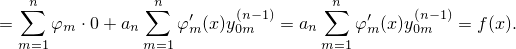∑n ∑n ′ (n-1) ∑n ′ (n-1) = φm ⋅0+ an φ m(x)y0m = an φm (x)y0m = f(x). m=1 m=1 m=1

(6)

Рассмотрим теперь вопрос о том, можем ли мы подобрать такие функции φ_m(x), чтобы они удовлеторяли одновременно (4) и уравнению (1) в вышеполученной форме (6). Для того, чтобы первая производная удовлетворяла и (3), и (4)

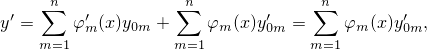
′ ∑n ′ n∑ ′ ∑n ′ y = φm(x)y0m + φm (x)y0m = φm (x)y0m, m=1 m=1 m=1

необходимо, чтобы

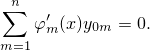
∑n ′ φm (x)y0m = 0. m=1

Аналогично, чтобы вторая производная удовлетворяла вышеупомянутым уравнениям

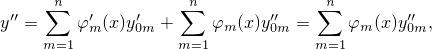
∑n ∑n ∑n y′′ = φ′m(x)y′0m + φm (x)y′0′m = φm(x)y′′0m, m=1 m=1 m=1

надо чтобы

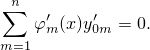
∑n φ′m (x)y′0m = 0. m=1

В общем случае

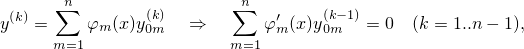
∑n ∑n y(k) = φm (x )y(0km) ⇒ φ′m(x)y(0k-m 1) = 0 (k = 1..n- 1), m=1 m=1

т.е.

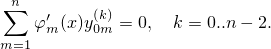
n ∑ φ′(x)y(k)= 0, k = 0..n - 2. m=1 m 0m

Эти уравнения дополняются уравнением (6)

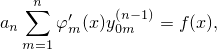
∑n ′ (n-1) an φm (x )y0m = f(x), m=1

и полученная таким образом система состоит из n линейных неоднородных уравнений, из которых мы находим n производных φ′_m(x). Эта задача имеет однозначное решение.

Для любопытных: коэффициенты в левой части образуют матрицу, определителем которой будет определитель Вронского для функций y_0m. Так как функции y_0m суть линейно независимые решения, их определитель Вронского будет не равен нулю, а следоватетельно, неоднородная система с такими коэффициентами имеет одно решение.

Найдя же производные φ′_m(x) и проинтегрировав полученное, можно найти сами функции φ_m(x). Подставив их в уравнение (3), мы получим функцию y, являющуюся решением уравнения (1).