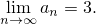Чтобы добро не пропало — решил набить для будущих поколений.
Найти предел
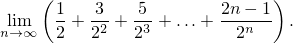
Элемент последовательности можно выразить в виде
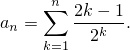
Тогда
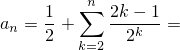
(заменим 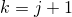 )
)
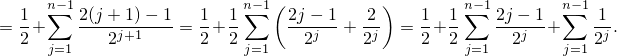
Второе слагаемое пропорционально 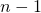 -му элементу последовательности
-му элементу последовательности
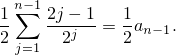
Последнее слагаемое – сумма геометрической прогрессии. Сумма геометрической прогрессии
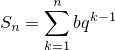
вычисляется по формуле

В данном случае
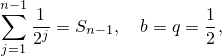
и
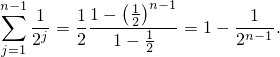
Следовательно,
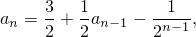
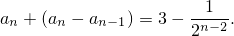
Вычислим теперь предел от обеих частей. Так как
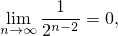
правая часть устремится к числу 3. Первое слагаемое левой части будет представлять собой искомый нами предел последовательности. Интереснее всего получается с разностью, взятой в скобки.
Если последовательность 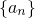 имеет предел, она должна удовлетворять
критерию Коши: для любого
имеет предел, она должна удовлетворять
критерию Коши: для любого  должно существовать такое
должно существовать такое 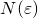 , что при
любых
, что при
любых  ,
, 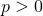
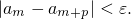
Рассмотрим частный случай. Пусть 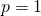 , также мы переобозначим
, также мы переобозначим
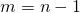 ,
, 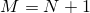 . Тогда при
. Тогда при 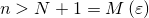 будет
будет
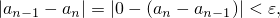
что по определению предела означает, что
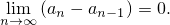
Учитывая это, мы приходим к тому, что