Вывод для гр. 620а, который я не успел сделать на занятии.
Как известно, комплексное число можно представить как в алгебраической, так и в
тригонометрической/показательной формах: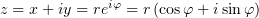 
.
Действительные числа, фиксирующие комплексное число при этих двух
способах его задания, связаны так:
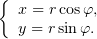 | (1) |
Рассмотрим теперь дифференцируемую функцию от этого числа:
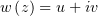. Её действительная и мнимая части удовлетворяют условиям
Коши-Римана:
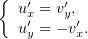 | (2) |
Но если записать число 
в показательной форме, то 
и 
становятся
функциями от переменных 
и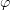 
.
На этот случай перепишем условия Коши-Римана для
тригонометрической/показательной формы записи аргумента. Итак, 
и 
зависят от переменных 
и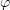 
, а те, в свою очередь, зависят от 
и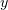 
. По
формуле дифференцирования сложной функции, зависящей от многих
аргументов, получим из (2)
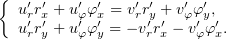 | (3) |
Осталось избавиться от производных новых переменных по старым. Для этого
возьмём (1) и продифференцируем сначала по 
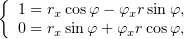
что потом решим относительно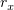 
и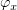 
:
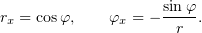
Теперь продифференцируем (1) по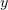 
:
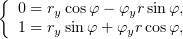
и решим эту систему относительно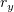
и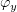 
:
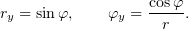
Теперь подставим найденные производные в (3), и выразим из системы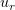 
и
:
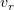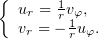
Этот вид условий Коши-Римана пригождается для случаев, когда аргумент функции представлен в тригонометрической либо показательной форме, и его перевод в алгебраическую фору по каким-то причинам нежелателен.
