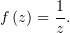Ещё одно пояснение для гр. 620а.
Условия Коши-Римана позволяют восстановить дифференцируемую функцию
по её действительной или мнимой части, если известно её значение в какой-либо
точке. Например, решить такую задачу:
Восстановить функцию 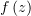 по действительной части
по действительной части
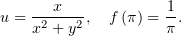
Действительная часть функции 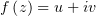 нам уже дана, и осталось найти
мнимую часть. Сделаем это, пользуясь тем, что части
нам уже дана, и осталось найти
мнимую часть. Сделаем это, пользуясь тем, что части  и
и  функции
функции 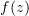 удовлетворяют условиям
удовлетворяют условиям
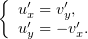 | (1) |
Зная  , получим
, получим
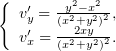
Интегрируя первое, получим общий вид  , который далее будем уточнять:
, который далее будем уточнять:
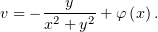
Подставим  во второе уравнение в (1)
во второе уравнение в (1)
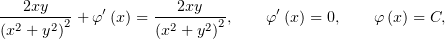
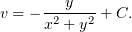
Отныне у нас есть всё необходимое для сборки 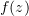 :
:
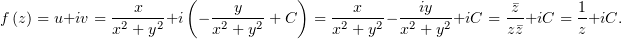
Осталось определить 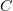 из значения функции в точке , указанного в условиях
задачи:
из значения функции в точке , указанного в условиях
задачи:
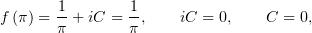
откуда окончательно