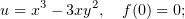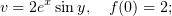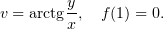Оно объёмное, поэтому советую приниматься раньше, чем начнётся вторая неделя до занятия.
Проверить на дифференцируемость и найти производные, если они есть, для экспоненты, а также тригонометрических и гиперболических функций.
Записав ветвь функци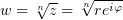и 
при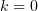 
, т.е.
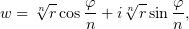
найти её область дифференцируемости и производную, воспользовавшись условиями Коши-Римана в полярных координатах.
По этому образцу восстановить дифференцируемые функции из действительных либо мнимых частей:
