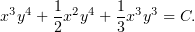Тов. Ларин интересовался, как решается первое уравнение из третьего варианта
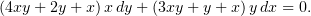
Решается оно так.
Раскроем скобки:
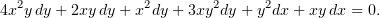 | (1) |
Сначала упакуем слагаемые третьей степени. Заметим, что
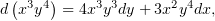
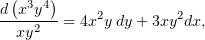
и сделаем соответствующую замену в уравнении (1):
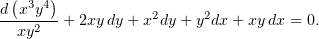 | (2) |
Теперь заметим, что
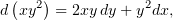
в связи с чем уравнение (2) приобретёт вид
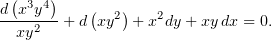 | (3) |
Наконец,
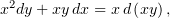
и применив это, можно получить из (3)
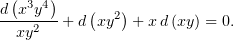 | (4) |
Умножим обе части на 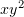 :
:
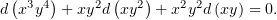 | (5) |
Произведём замену
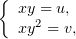
после которой уравнение (5) приобретёт легко интегрируемый (и уже частично интегрированный) вид:
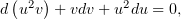
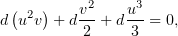
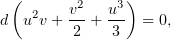
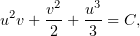
откуда обратной заменой получаем окончательный результат: