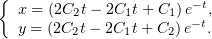Решить систему
 | (1) |
Выпишем матрицу этой системы:
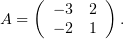
Не описывая подробно хорошо знакомый с первого курса процесс получения
собственных значений и собственных векторов матриц, отметим, что у матрицы
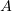 имеется одно собственное значение
имеется одно собственное значение 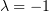 кратности 2, и ему принадлежит
один линейно независимый собственный вектор
кратности 2, и ему принадлежит
один линейно независимый собственный вектор
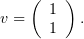
Т.е. алгебраическая кратность 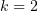 , а геометрическая
, а геометрическая 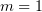 . Значит,
следует искать решения системы (1), относящиеся к корню
. Значит,
следует искать решения системы (1), относящиеся к корню 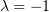 (других
решений у этой системы нет) в виде (на всякий случай: верхние индексы не означают степеней)
(других
решений у этой системы нет) в виде (на всякий случай: верхние индексы не означают степеней)
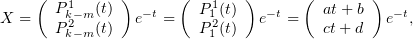 | (2) |
или, в невекторном виде,
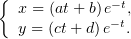 | (3) |
Подставим вышеприведённые функции в систему (1), сократим 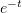 и
получим
и
получим
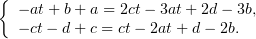
Так как эти равенства должны соблюдаться при любых значениях 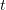 , должны
быть равны коэффициенты при равных степенях левых и правых частей
соответственно:
, должны
быть равны коэффициенты при равных степенях левых и правых частей
соответственно:
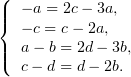
Из первого и второго уравнений (они эквивалентны) следует, что  , а из
третьего и четвёртого - что
, а из
третьего и четвёртого - что 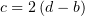 . Никаким образом уточнить
оставшиеся два коэффициента при помощи этой системы невозможно. С учётом
полученных связей между коэффициентами можно переписать (2) в
виде
. Никаким образом уточнить
оставшиеся два коэффициента при помощи этой системы невозможно. С учётом
полученных связей между коэффициентами можно переписать (2) в
виде
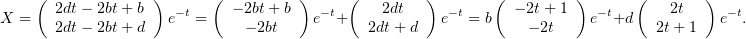
Выбирая различные значения  и
и 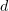 , можно выделять пары независимых
частных решений. Например,
, можно выделять пары независимых
частных решений. Например,
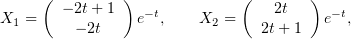
и тогда общее решение первоначальной системы (1) можно записать, просто
заменив 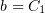 и
и 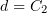 :
:
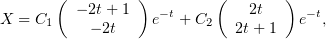
или, в виде отдельных функций,