Тов. Ларин интересовался, как решается первое уравнение из третьего варианта
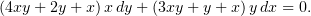
Решается оно так.
Тов. Ларин интересовался, как решается первое уравнение из третьего варианта
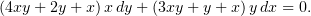
Решается оно так.
Оно объёмное, поэтому советую приниматься раньше, чем начнётся вторая неделя до занятия.
Проверить на дифференцируемость и найти производные, если они есть, для экспоненты, а также тригонометрических и гиперболических функций.
Записав ветвь функции 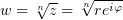 при
при 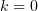 , т.е.
, т.е.
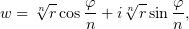
найти её область дифференцируемости и производную, воспользовавшись условиями Коши-Римана в полярных координатах.
По этому образцу восстановить дифференцируемые функции из действительных либо мнимых частей:
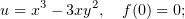
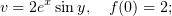

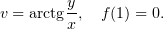
Ещё одно пояснение для гр. 620а.
Условия Коши-Римана позволяют восстановить дифференцируемую функцию
по её действительной или мнимой части, если известно её значение в какой-либо
точке. Например, решить такую задачу:
(more…)
Филиппов А.Ф. «Сборник задач по дифференциальным уравнениям»; номера: 155 — 158, 168 — 170.
Филиппов А.Ф. «Сборник задач по дифференциальным уравнениям»; номера: 427 — 431, 458, 459, 465, 466, 475, 476.
Филиппов А.Ф. «Сборник задач по дифференциальным уравнениям»; номера: 529 — 532, 539 — 543, 576, 577.
Контрольная работа по диф.уравнениям первого порядка в гр. 6211 будет 16 октября 2013 года.
Готовьтесь!
Хостингом угостил Вадим "Moose" Калинников