Найти веторный потенциал поля 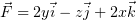 .
.
Во-первых, скажем пару слов о произволе решения. Если произвол при нахождении скалярного потенциала у нас получился в качестве побочного продукта в конце решения, то произвол векторного становится нужен практически немедленно.
Так как 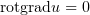 , прибавив к векторному потенциалу
, прибавив к векторному потенциалу 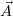 соленоидального
поля
соленоидального
поля 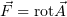 , мы получим векторное поле, также являющееся векторным
потенциалом поля
, мы получим векторное поле, также являющееся векторным
потенциалом поля 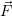 :
:
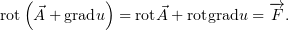
Таким образом, у одного поля 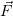 имеется целое семейство потенциалов,
отличающихся градиентным слагаемым.
имеется целое семейство потенциалов,
отличающихся градиентным слагаемым.
Итак, пусть поле 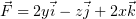 имеет потенциал
имеет потенциал 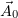 :
: 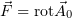 ,
или
,
или
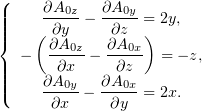 | (1) |
Очень не хочется на втором курсе решать систему неоднородных уравнений в
частных производных. Они и по-отдельности не подарок, а уж в системах тем
более. Поэтому будем хитрить. Предположим, что эта задача имеет решение,
причём 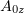 интегрируемо по
интегрируемо по  , то есть существует такое
, то есть существует такое 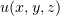 ,
что
,
что 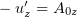 . Рассмотрим новое поле
. Рассмотрим новое поле 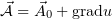 . Оно тоже
является потенциалом поля
. Оно тоже
является потенциалом поля 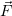 и удовлетворяет системе (1), но у него
и удовлетворяет системе (1), но у него
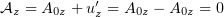 (А.М. Анчиков, судя по ответу, уничтожал
(А.М. Анчиков, судя по ответу, уничтожал
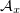 ). Значит, для второго рассматриваемого потенциала система (1)
превратится в такую:
). Значит, для второго рассматриваемого потенциала система (1)
превратится в такую:
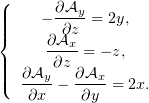 | (2) |
Проинтегрировав первые два уравнения, получим, что
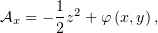
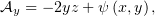
причём
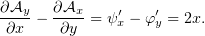
Таким образом, для нахождения потенциала осталось определить функции
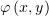 и
и 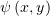 . Они тоже определяются из неоднородного уравнения в
частных производных, которое, правда, тут уже одно. Чтобы от него
избавиться, применим ту же хитрость ещё один раз. Предположим, что и эта
задача имеет решение, причём
. Они тоже определяются из неоднородного уравнения в
частных производных, которое, правда, тут уже одно. Чтобы от него
избавиться, применим ту же хитрость ещё один раз. Предположим, что и эта
задача имеет решение, причём 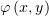 интегрируемо по
интегрируемо по  , то есть
существует такое
, то есть
существует такое 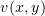 , что
, что 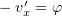 . Рассмотрим уже третьего
кандидата в потенциалы: поле
. Рассмотрим уже третьего
кандидата в потенциалы: поле 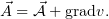 Сказать про него мы можем
следующее:
Сказать про него мы можем
следующее:
- Оно является потенциалом поля
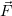 , т.е.
, т.е. 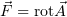 , так как оно
получено добавлением к потенциалу
, так как оно
получено добавлением к потенциалу 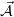 градиентной добавки;
градиентной добавки;
- Оно имеет нулевую компоненту
 , т.к.
, т.к. 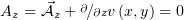 .
.
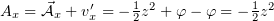 .
.
Раскладывая по компонентам уравнение 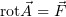 , и учитывая, что
, и учитывая, что 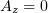 и
и
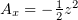 , получим:
, получим:
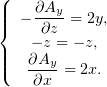 | (3) |
Второе уравнение тривиально, из первого получим 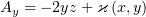 , что в
третьем уравнении даст
, что в
третьем уравнении даст 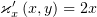 , таким образом,
, таким образом, 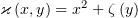 и
и
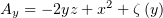 . Вычитанием из полученного потенциала градиента от
первообразной
. Вычитанием из полученного потенциала градиента от
первообразной 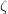 можно получить потенциал с такими компонентами:
можно получить потенциал с такими компонентами:
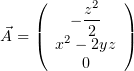
Любопытно, что в ответе у А.М. Анчикова значится потенциал
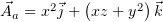 . Разность моего потенциала и потенциала Анчикова
даёт
. Разность моего потенциала и потенциала Анчикова
даёт
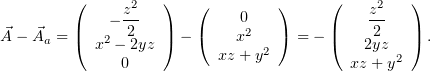
Заметим, что 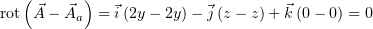 . Таким
образом, мой ответ отличается от ответа Анчикова на некий градиент,
и следовательно, они принадлежат к одному семейству потенциалов.
. Таким
образом, мой ответ отличается от ответа Анчикова на некий градиент,
и следовательно, они принадлежат к одному семейству потенциалов.
