За неимением времени я не доказывал формулу для квадрата суммы многих слагаемых
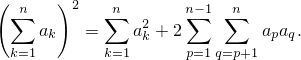 | (1) |
Для тех, кому интересно, могу доказать.
Докажем методом мат.индукции. При 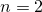 , как известно,
, как известно,
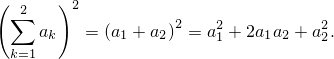
По формуле (1) получается
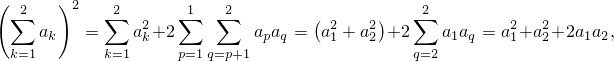
т.е. формула (1) для 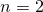 выполняется.
выполняется.
Теперь выполним шаг индукции. Пусть для 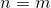 формула (1) считается
доказанной:
формула (1) считается
доказанной:
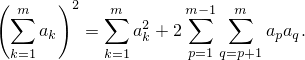 | (2) |
Докажем её при 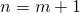 , т.е. что
, т.е. что
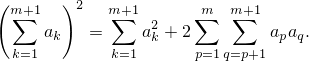 | (3) |
Начнём преобразовывать левую часть (3):
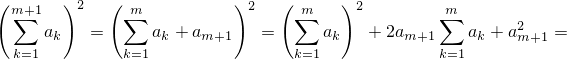
согласно формуле (2)
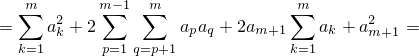
объединим квадраты
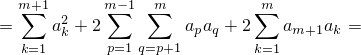
отсоединим от последней суммы последнее слагаемое и заменим переменную суммирования
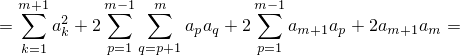
объединим суммы посередине, последнее слагаемое перепишем в виде двойной суммы из одного слагаемого (потом пригодится)
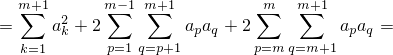
суммы по соседствующим диапазонам чисел слипаются, и получается
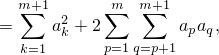
что совпадает с правой частью (3).
Шаг индукции сделан, формула доказана.
