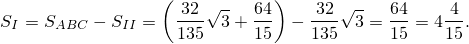В новой нумерации, вероятно, эта задача называется 2424 в)
Найти площадь фигуры, ограниченной линиями:
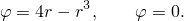
Исследовав функцию 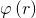 , обнаружим, что
, обнаружим, что 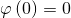 и при положительном
и при положительном
 она имеет один максимум, после чего начинает убывать. Она снова доходит
до нуля при
она имеет один максимум, после чего начинает убывать. Она снова доходит
до нуля при 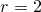 и дальше стремиться к
и дальше стремиться к 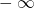 . Точка максимума
достигается при
. Точка максимума
достигается при 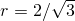 , и в ней
, и в ней 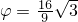 . Нетрудно убедиться, что
. Нетрудно убедиться, что
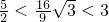 . В полярных координатах множество точек, у которых
координата
. В полярных координатах множество точек, у которых
координата 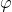 зависит от
зависит от  именно таким образом, образует такую
кривую:
именно таким образом, образует такую
кривую:
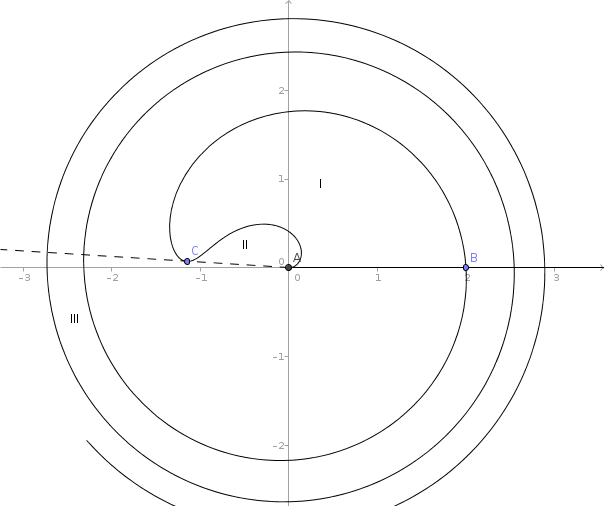
Вообще говоря, линии 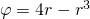 и
и 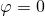 ограничивают бесконечное
множество замкнутых областей, в том числе, область III и остальные подобные
ей. Мы найдём площадь области I. Эта область, заметим, образуется изъятием
области II из сектора
ограничивают бесконечное
множество замкнутых областей, в том числе, область III и остальные подобные
ей. Мы найдём площадь области I. Эта область, заметим, образуется изъятием
области II из сектора 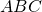 , поэтому
, поэтому
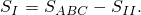
Найдём отдельно 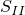 и
и 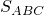 , пользуясь тем, что оба являются
криволинейными секторами. Площадь криволинейного сектора вычисляется по
формуле
, пользуясь тем, что оба являются
криволинейными секторами. Площадь криволинейного сектора вычисляется по
формуле
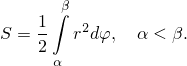
Участок кривой, ограничивающей сектор II, соединяет точки 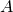 и
и 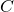 , и
меньшее значение
, и
меньшее значение 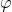 соответствует точке
соответствует точке 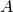 . Поэтому
. Поэтому
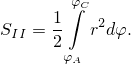
Дальше мы перейдём к переменной интегрирования  пользуясь тем, что
пользуясь тем, что
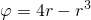 :
:
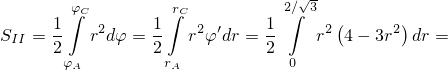
![√ - -
1 2∫∕ 3( ) 1 (4 3 )||2∕√ 3 1 [4( 2 )3 3( 2 )5] 32 √-
= - 4r2 − 3r4 dr =- -r3 − -r5 || = - - √-- − - √-- = --- 3.
2 0 2 3 5 0 2 3 3 5 3 135](http://shine.ylsoftware.com/math-img/dem2424-3/dem2424-326x.png)
Участок кривой, ограничивающей сектор 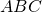 , соединяет точки
, соединяет точки 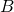 и
и 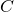 ,
меньшее значение
,
меньшее значение 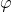 соответствует точке
соответствует точке 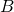 , поэтому
, поэтому
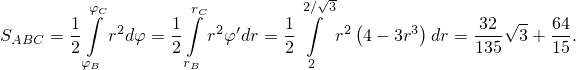
Окончательно