То, что на занятии я пытался объяснить быстро. Если объяснять небыстро, получается так:
Исследовать на сходимость интеграл
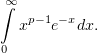 | (1) |
Рассмотим случаи:
1) 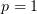 В этом случае интеграл (1) найти легко:
В этом случае интеграл (1) найти легко:
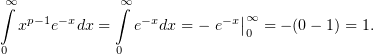
2) 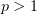 Обозначим
Обозначим 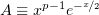 ,
, 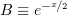 . Разложим подынтегральное
выражение на множители
. Разложим подынтегральное
выражение на множители
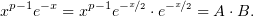
Легко заметить, что при 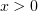
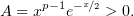 | (2) |
Исследуем 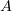 на промежутки монотонности:
на промежутки монотонности:
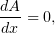
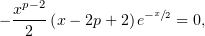
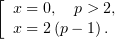
На промежутке 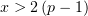
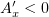 , следовательно, функция
, следовательно, функция 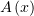 убывает
при
убывает
при 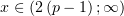 . При
. При 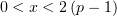 функция
функция 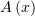 возрастает,
следовательно, наибольшего значения в интервале
возрастает,
следовательно, наибольшего значения в интервале 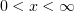 она достигает в
точке
она достигает в
точке 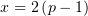 .
.
Обозначим 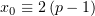 . В силу убывания
. В силу убывания 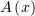 , если
, если 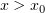 , то
, то
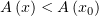 . Заметим, что и
. Заметим, что и 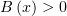 , и пользуясь этим, умножим
последнее неравенство на
, и пользуясь этим, умножим
последнее неравенство на 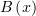 :
:
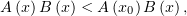
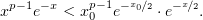 | (3) |
Так как 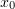 – константа, бОльшая функция легко интегрируется на интервале
– константа, бОльшая функция легко интегрируется на интервале
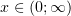 :
:
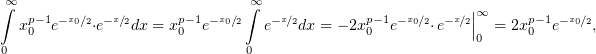
т.е. несобственный интеграл от неё сходится. Отсюда, в силу (2) и (3), по первому признаку сравнения, сходится интеграл (1).
3) 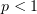 В этом случае проблем становится две: кроме бесконечности в
верхнем пределе интегрирования подынтегральная функция стремится к
бесконечности в нуле. Разобъём интеграл на два:
В этом случае проблем становится две: кроме бесконечности в
верхнем пределе интегрирования подынтегральная функция стремится к
бесконечности в нуле. Разобъём интеграл на два:
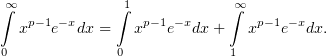
Относительно второго интеграла заметим, что 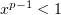 при
при  и
и 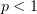 ,
следовательно,
,
следовательно, 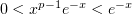 ; интеграл мажорирующей функции
сходится, и следовательно второй интеграл сходится. В первом интеграле
заменим переменные по формуле
; интеграл мажорирующей функции
сходится, и следовательно второй интеграл сходится. В первом интеграле
заменим переменные по формуле 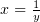 :
:
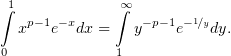 | (4) |
При
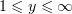
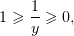
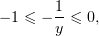
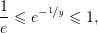
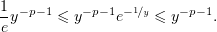 | (5) |
Далее есть смысл рассмотреть такие случаи:.
3.1) 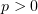 Про мажорирующую функцию можно установить, что
Про мажорирующую функцию можно установить, что
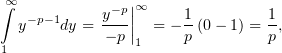
её интеграл сходится, значит и интеграл (4) сходится.
3.2) 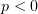
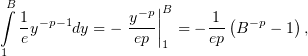
найденная первообразная при 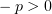 и
и 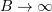 стремится к бесконечности:
стремится к бесконечности:
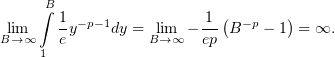
Но, по (5),
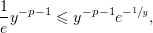
значит,
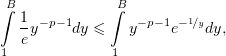
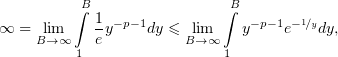
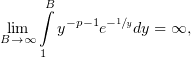
т.е. интеграл (4) не сходится.
3.3) Отдельно рассмотрим частный случай 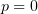 . Интеграл (4) в этом
случае приобретает вид
. Интеграл (4) в этом
случае приобретает вид
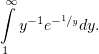
Согласно (5),
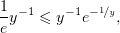
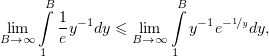
но
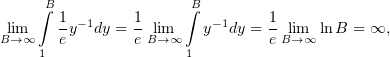
откуда, по тем же соображениям, что и в предыдущем случае, следует расходимость интеграла (4).
Мы получили, что в случае 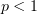 , исходный интеграл (1) раскладывается на
два несобственных интеграла, один из которых сходится всегда, а второй
сходится только при
, исходный интеграл (1) раскладывается на
два несобственных интеграла, один из которых сходится всегда, а второй
сходится только при 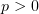 . Значит, интеграл (1) сходится при
. Значит, интеграл (1) сходится при 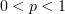 . До
этого мы получили, что он сходится также при
. До
этого мы получили, что он сходится также при 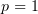 и
и 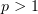 . Следовательно,
он сходится при всех
. Следовательно,
он сходится при всех 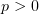 .
.
