Эту задачу на занятии с гр. №304 мы начали делать, считая на границах саму искомую функцию равной нулю. Занятие это было тоже небесполезно, но в самой задаче граничные условия были другими: справа занулялась производная. Задачи с разными граничными условиями встречаются, однако, нередко, так что желательно знать, как они решаются. Итак:
Найти решение уравнения:
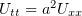 | (1) |
Граничные условия:
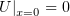 | (2) |
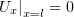 | (3) |
Начальные условия:
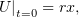 | (4) |
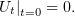 | (5) |
Как и раньше, решим сначала задачу с однородными условиями: найдём все
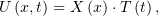 | (6) |
удовлетворяющие уравнению колебаний и граничным условиям. Уравнение колебаний даст снова
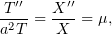
где 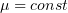 .
.
1 Пространственная часть
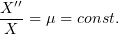
Характеристическое уравнение:
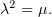
Рассмотрим случаи:
1.1 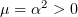
Тогда 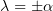 ,
,
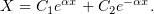
Из левого граничного условия
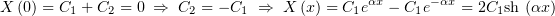
Но при 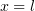 мы должны обнулить производную
мы должны обнулить производную 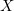 :
:
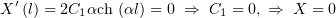
– решения получаются только нулевые.
1.2 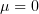
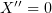 ,
, 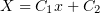 ,
,
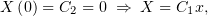
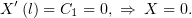
1.3 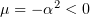
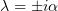 ,
,
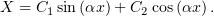
Граничные условия:
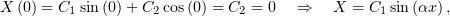
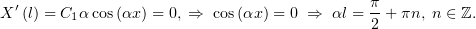
Следовательно только для отрицательных 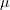 существуют ненулевые решения, причём такие:
существуют ненулевые решения, причём такие:
![[ ]
X = Cn sin π(1+-2n)x .
n 1 2l](http://shine.ylsoftware.com/math-img/dn26/dn2628x.png)
Каждому семейству решений для отрицательного значения 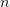 соответствует равное семейство для неотрицательного
соответствует равное семейство для неотрицательного
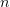 , поэтому достаточно рассмотреть
, поэтому достаточно рассмотреть
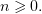
При этом
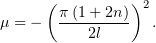
2 Временная часть
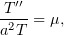 | (7) |
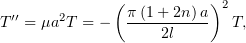 | (8) |
![n [π(1+-2n)a-] n [π-(1+-2n)a ]
Tn = C3 cos 2l t + C4 sin 2l t .](http://shine.ylsoftware.com/math-img/dn26/dn2635x.png) | (9) |
3 Общее решение
Теперь, согласно (6), получим решения уравнения колебаний с граничными условиями:
![[ ]{ [ ] [ ]}
n π-(1-+-2n) n π-(1+-2n)a n π-(1-+-2n)a
Un = XnTn = C 1 sin 2l x C 3 cos 2l t + C 4 sin 2l t .](http://shine.ylsoftware.com/math-img/dn26/dn2636x.png)
Сумма таких функций тоже удовлетворяет уравнению колебаний с граничными условиями:
![∞ ∞ [ ]{ [ ] [ ]}
U = ∑ U = ∑ sin π-(1-+-2n)x Cn cos π-(1+-2n)at + Cn sin π-(1-+-2n)at ,
n=0 n n=0 2l 5 2l 6 2l](http://shine.ylsoftware.com/math-img/dn26/dn2637x.png) | (10) |
где переобозначено 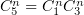 ,
, 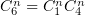 .
.
В начальный момент времени 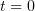 имеем
имеем
![∑∞ [π-(1+-2n) ] n n ∞∑ n [π(1+-2n)-]
U |t=0 = sin 2l x {C 5 ⋅1 +C 6 ⋅0} = C5 sin 2l x ,
n=0 n=0](http://shine.ylsoftware.com/math-img/dn26/dn2641x.png) | (11) |
![|
∂ ∑∞ [π (1+ 2n) ]{ n [ π(1+ 2n)a ] n [π (1+ 2n)a ]}||
Ut|t=0 = ∂t sin ----2l---x C5 cos ----2l----t + C6 sin----2l----t || =
n=0 t=0](http://shine.ylsoftware.com/math-img/dn26/dn2642x.png)
![|
∑∞ [π (1 + 2n) ]{ π(1+ 2n) a [π(1 +2n )a ] π(1+ 2n)a [π(1 +2n )a ]}||
= sin ----2l---x − Cn5----2l----sin ----2l----t + Cn6 ----2l----cos ----2l----t || =
n=0 t=0](http://shine.ylsoftware.com/math-img/dn26/dn2643x.png) | (12) |
![∞∑ [ ] { } ∑∞ [ ]
= sin π(1+-2n)x Cn6 π(1+-2n)a-⋅1 = Cn6 π(1-+2n-)asin π-(1-+-2n-)x .
n=0 2l 2l n=0 2l 2l](http://shine.ylsoftware.com/math-img/dn26/dn2644x.png)
4 Начальные условия
4.1 Начальная скорость
![∑∞ nπ-(1-+-2n)a [π-(1-+-2n) ]
Ut|t=0 = C 6 2l sin 2l x = 0.
n=0](http://shine.ylsoftware.com/math-img/dn26/dn2645x.png)
Умножив обе части на ![[ ]
sin π(1+2πm)x
2l](http://shine.ylsoftware.com/math-img/dn26/dn2646x.png) и проинтегрировав обе части по отрезку
и проинтегрировав обе части по отрезку 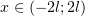 , в правой части мы
получим
, в правой части мы
получим 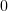 , а в левой
, а в левой
![∫2l∞ [ ] [ ]
∑ Cnπ-(1+-2n)a sin π-(1+-2n)x sin π-(1+-2m)x dx =
n=0 6 2l 2l 2l
2l](http://shine.ylsoftware.com/math-img/dn26/dn2649x.png)
![∑∞ ∫2l [ ] [ ]
= Cn6π (1 + 2n)a 1 sin π-(1-+-2n)x sin π-(1-+-2m)x dx =
n=0 2l2l 2l 2l](http://shine.ylsoftware.com/math-img/dn26/dn2650x.png)
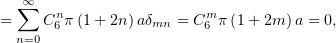
и заменив  , мы получим, что
, мы получим, что 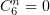 , а значит (по (10)),
, а значит (по (10)),
![∑∞ n [π(1+-2n)-] [π(1+-2n)-a]
U = C5 sin 2l x cos 2l t .
n=0](http://shine.ylsoftware.com/math-img/dn26/dn2654x.png) | (13) |
4.2 Начальное отклонение
![∞ [ ]
∑ Cn sin π(1+-2n)x = rx.
n=0 5 2l](http://shine.ylsoftware.com/math-img/dn26/dn2655x.png) | (14) |
В левой части стоит ряд Фурье – но прежде чем находить его коэффициенты, требуется ещё определить, по какому
промежутку и какая функция раскладывалась в этот ряд (не спешите оглядываться на правую часть). В знаменателе
аргумента синуса стоит 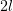 - значит, разложение велось на отрезке
- значит, разложение велось на отрезке ![x ∈ [− 2l;2l]](http://shine.ylsoftware.com/math-img/dn26/dn2657x.png) . Общий вид подобного разложения
будет таким:
. Общий вид подобного разложения
будет таким:
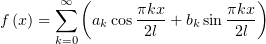
Наличие в разложении (14) одних только синусов указывает на нечётность раскладываемой функции. Но кроме того,
слагаемые в нём имеют исключительно нечётные номера: 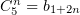 . Подумаем, разложение какой нечётной функции
на таком отрезке привело бы к обнулению коэффициентов с чётными номерами:
. Подумаем, разложение какой нечётной функции
на таком отрезке привело бы к обнулению коэффициентов с чётными номерами:
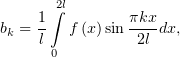
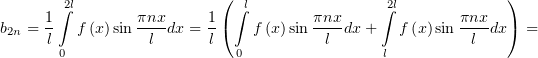
Заменим в первом интеграле 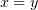 , а во втором –
, а во втором – 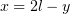 :
:
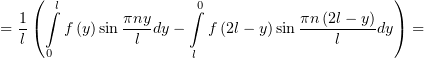
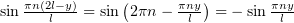
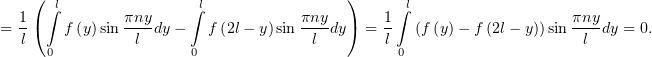
Таким свойством определённо обладает функция, для которой
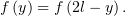 | (15) |
Но функция в правой части (14) определена лишь на отрезке 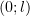 , за пределами которого мы можем доопределять её
как хотим. Пусть раскладываемая в ряд Фурье функция будет определяться так:
, за пределами которого мы можем доопределять её
как хотим. Пусть раскладываемая в ряд Фурье функция будет определяться так:
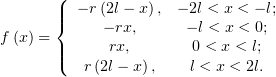
Для большей понятности приводится её график:
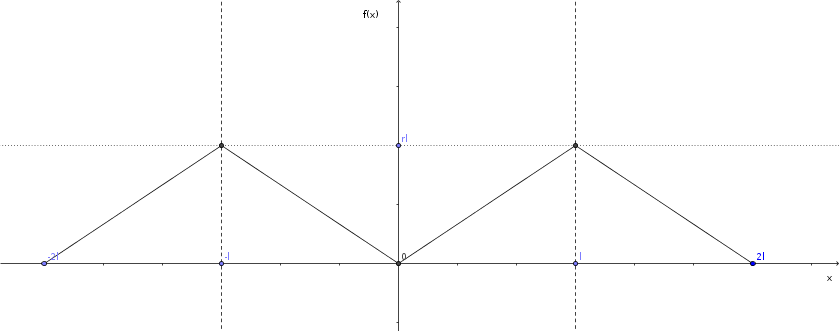
Тогда она будет и нечётной, и соответствовать (15). Коэффициенты 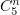 , единственные ненулевые в
разложении, найдутся по формуле
, единственные ненулевые в
разложении, найдутся по формуле
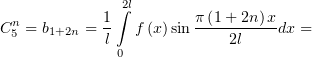
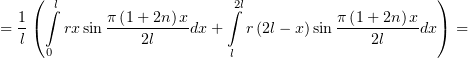
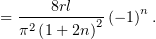
Подставляем этот результат в (13), и получаем:
![[ ] [ ]
8rl∞∑ -(−-1)n-- π-(1-+-2n) π-(1+-2n)a
U = π2 (1+ 2n)2 sin 2l x cos 2l t .
n=0](http://shine.ylsoftware.com/math-img/dn26/dn2674x.png)
Этот ответ, как и полученный на занятии, не совпадает с ответом в методичке. Однако это расстраивает нас мало, т.к. последний (при ближайшем рассмотрении) не удовлетворяет правому граничному условию.
