Страница сетевой поддержки учеников Тимура Юрьевича Альпина

30.10.2015

Даишев, Никитин №71

Filed under: ММФ,Решения — Shine @ 12:25 пп

Решить уравнение

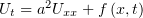Ut = a2Uxx + f (x,t)
(1)

при начальном условии

U|t=0 = 0.
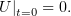(2)

Обозначим, как обычно,

∞∫ ¯U = √1-- U e−ixydx, 2π −∞

∫∞ ¯f = √1-- fe−ixydx, 2π −∞
(3)

Обе части уравнения (1) домножим на −ixy e , проинтегрируем по x от − ∞ до ∞ и разделим на √--- 2π :

∫∞ ∞∫ ∫∞ √1-- Ute−ixydx = a2√-1-- Uxxe− ixydx+ √1-- f (x,t)e−ixydx, 2π −∞ 2π−∞ 2π− ∞

∫∞ ¯Ut = a2 √1- Uxxe−ixydx + ¯f. 2π− ∞
(4)

Вычислим интеграл

∫∞ −ixy − ixy|∞ ∫∞ −ixy ∞∫ −ixy −ixy|∞ 2 ∫∞ −ixy Uxxe dx = Uxe |− ∞− (− iy) Uxe dx = (iy) Uxe dx = (iy) U e |−∞+ (iy) Ue dx = − ∞ −∞ −∞ −∞

2∫∞ − ixy 2√--- = − y U e dx = − y 2π ¯U. −∞

Тогда уравнение (4) преобразуется в такое:

2 2 ¯Ut = − a y ¯U +f¯,
(5)

т.е. в линейное неоднородное уравнение первого порядка. Как обычно, заменим

¯U = uv,
(6)

где u – частное решение однородного уравнения

ut = − a2y2u.

ln|u| = − a2y2t+ ˜C,

−a2y2t u = Ce .

Выберем частное решение с C = 1 :

u = e−a2y2t.

Заменим, согласно (6),

22 ¯U = ve−a yt.
(7)

Подставляем (7) в (5):

vte−a2y2t − a2y2ve−a2y2t = − a2y2ve−a2y2t +f¯,

2 2 vte−a y t = ¯f,

a2y2t vt = f¯(y,t)e ,

∫t v = ¯f (y,s)ea2y2sds, t0

и тогда

∫t ¯U = e−a2y2t f¯(y,s)ea2y2sds. t0
(8)

Начальное условие (2) приводит к тому, что:

| | 1 ∫∞ || 1 ∫∞ ¯U|t=0 = √--- Ue−ixydx|| = √--- U |t=0e−ixydx = 0. 2π− ∞ |t=0 2π −∞

Но из (8) следует, что

| 0∫ 22 U¯|t=0 = ¯f (y,s)eay sds, t0

в итоге

0 ∫ ¯ a2y2s f (y,s) e ds = 0. t0

Пользуясь последним, преобразуем (8):

( ∫t ) (∫t ∫0 ) ¯U = e−a2y2t( f¯(y,s)ea2y2sds− 0) = e− a2y2t( ¯f (y,s)ea2y2sds− f¯(y,s)ea2y2sds) = t0 t0 t0

( ∫t ∫t0 ) ∫t = e−a2y2t( f¯(y,s)ea2y2sds+ ¯f (y,s)ea2y2sds) = e−a2y2t f¯(y,s)ea2y2sds, t0 0 0

а вспомнив (3), заменим ¯f :

( ) ( ) 22 ∫t 1 ∫∞ 22 e− a2y2t∫t 22 ∫∞ ¯U = e−ay t √---( f (z,s)e−izydz) eay sds =-√--- ea ys( f (z,s)e−izydz) ds. 0 2π −∞ 2π 0 − ∞

Получив фурье-образ решения, найдём само решение U :

1 ∫∞ U = √--- ¯U eixydy = 2π −∞

∞∫ ( ∫t ) ∫∞ (∫t ) -1--- ( −a2y2t ¯ a2y2s ) ixy --1-- ( − a2y2t ¯ a2y2sixy ) = √ 2π e f (y,s)e ds e dy = √ 2π e f (y,s)e e ds dy = −∞ 0 −∞ 0

∫t( ∞∫ ) ∫t( ∞∫ ) = √1--- ( e−a2y2tf¯(y,s)ea2y2seixydy) ds = √1--- ( ¯f (y,s) ea2y2(s−t)eixydy) ds. 2π 2π 0 −∞ 0 −∞

Комментариев нет »

No comments yet.

RSS feed for comments on this post.

Leave a comment

Для отправки комментария вам необходимо авторизоваться.

Хостингом угостил Вадим "Moose" Калинников