Неделю назад я был неправ в одном моменте.
Я начал было доказывать, что если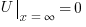 
, то и 
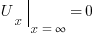. И не доказал. Что не странно, ибо есть контрпримеры.
Например, функция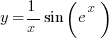 
имеет производную 
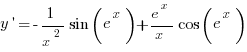. И хотя 
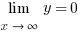, в производной 
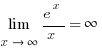, и сама производная не имеет предела на бесконечности.
Значит, в задачах на преобразования Фурье мы будем искать такие решения, которые будут обращаться в ноль на бесконечности вместе со своими производными, т.е. обнуления производных придётся требовать отдельно.
