Переходя к полярным координатам, найти объемы тел, ограниченных следующими
поверхностями:
\[
z^{2}=xy,\quad x^{2}+y^{2}=a^{2}.
\]
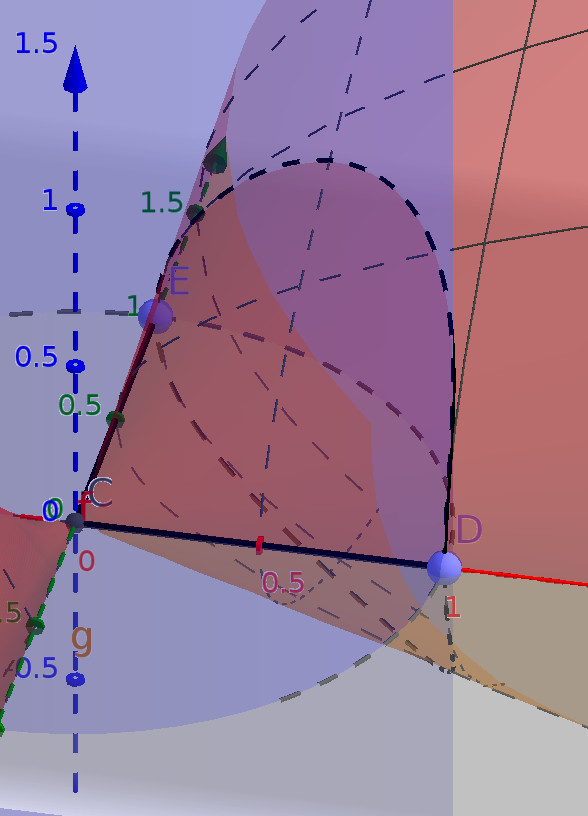
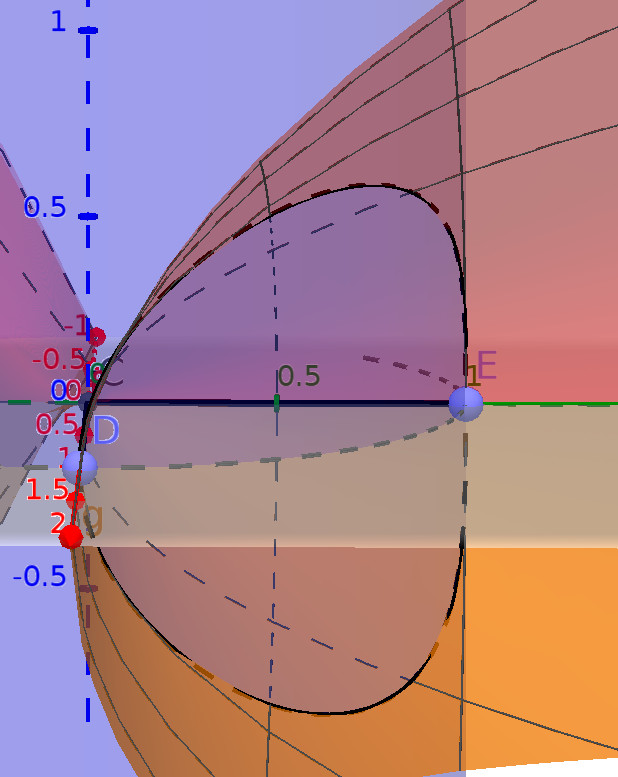
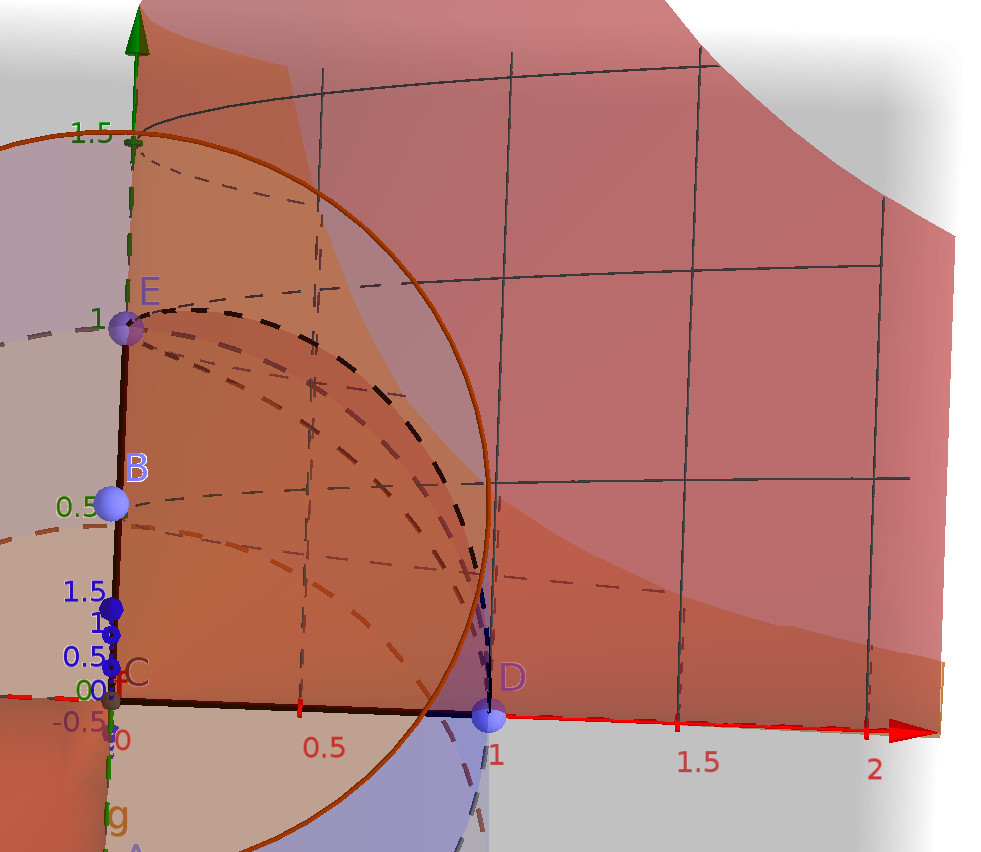
Как смог, я нарендерил эту фигуру в геогебре. Тут синим цветом показана цилиндрическая поверхность, серо-розовым — $z_1$, жёлтым — $z_2$. Нужная нам фигура лежит в первой четверти.

\[
z_{1}=\sqrt{xy},\qquad z_{2}=-\sqrt{xy}
\]
\[
V=\underset{\Omega}{\iint}\left(z_{1}-z_{2}\right)dxdy=\underset{\Omega}{\iint}2\sqrt{xy}dxdy
\]
Полярные координаты связаны с декартовыми, как обычно
\[
\left\{ \begin{array}{l}
x=r\cos\varphi,\\
y=r\sin\varphi;
\end{array}\right.
\]
их якобиан вычислялся ранее на занятиях
\[
\left|J\right|=r.
\]
Переходя к ним, получим
\[
V=\intop_{0}^{\pi/2}d\varphi\intop_{0}^{a}dr 2\sqrt{r\cos\varphi r\sin\varphi}r=2\intop_{0}^{\pi/2}d\varphi\sqrt{\cos\varphi\sin\varphi}\intop_{0}^{a}drr^{2}=
\frac{2a^{3}}{3}\intop_{0}^{\pi/2}\sqrt{\cos\varphi\sin\varphi}d\varphi.
\]
Заменим
$\sin^{2}\varphi=t$
\[
V=\frac{2a^{3}}{3}\intop_{0}^{\pi/2}\sqrt{\cos\varphi\sin\varphi}d\varphi=
\frac{2a^{3}}{3}\intop_{0}^{\pi/2}\cos^{-1/2}\varphi\sin^{-1/2}\varphi\cos\varphi\sin\varphi d\varphi=
\frac{2a^{3}}{6}\intop_{0}^{\pi/2}\left(\sin^{2}\varphi\right)^{-1/4}\left(\cos^{2}\varphi\right)^{-1/4}\left(\sin^{2}\varphi\right)'d\varphi=
\]
\[
=
\frac{2a^{3}}{6}\intop_{0}^{1}t^{-1/4}\left(1-t\right)^{-1/4}dt=
\frac{2a^{3}}{6}\intop_{0}^{1}t^{3/4-1}\left(1-t\right)^{3/4-1}dt=
\frac{2a^{3}}{6}B\left(\frac{3}{4},\frac{3}{4}\right)=
\]
(здесь $B\left(\frac{3}{4},\frac{3}{4}\right)$ — это интеграл Эйлера 1-го рода)
\[
=\frac{2a^{3}}{6}\frac{\Gamma\left(\frac{3}{4}\right)\Gamma\left(\frac{3}{4}\right)}{\Gamma\left(\frac{6}{4}\right)}=\frac{2a^{3}\Gamma^{2}\left(\frac{3}{4}\right)}{3\sqrt{\pi}}.
\]
В более простом виде ответ не представляется.
