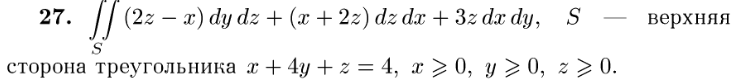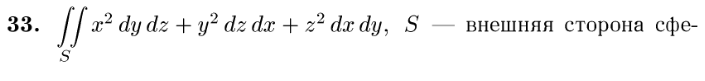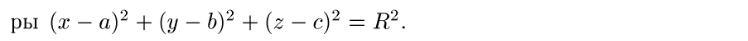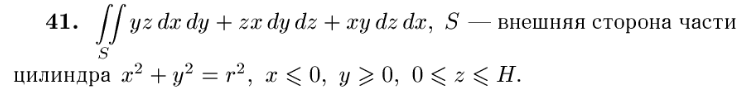При определении поверхностных интегралов первого рода использовался модуль вектора $\overrightarrow{dS}$. Для параметрически заданной поверхности он равнялся $\overrightarrow{dS}$=$\left[\vec{r}_{u}^{\prime}\times\vec{r}_{v}^{\prime}\right]dudv$.
Поверхностный интеграл второго рода использует сам вектор $\overrightarrow{dS}$, на который скалярно умножается интегрируемая векторная величина \[ \overrightarrow{F}=\left(\begin{array}{c} P\left(x,y,z\right)\\ Q\left(x,y,z\right)\\ R\left(x,y,z\right) \end{array}\right). \] Компоненты вектора $\overrightarrow{dS}$ традиционно обозначаются так: \[ \overrightarrow{dS}=\left(\begin{array}{c} dydz\\ dxdz\\ dxdy \end{array}\right), \] и при умножении на подынтегральное выражение они умножаются на соответствующие компоненты вектора $\overrightarrow{F}$. Так что если, например, вы видите интеграл второго рода такой: \[ \iint\limits _{S}\left(zdxdy+ydxdz+xdydz\right), \] то интегрируется \[ \overrightarrow{F}=\left(\begin{array}{c} x\\ y\\ z \end{array}\right), \] т.е. $P=x$, $Q=y$, $R=z$.
Так как пара параметров $u$ и $v$ не предполагает строгой очерёдности, а от порядка множителей векторного произведения зависит его направление, при постановке задач требуется уточнять направление вектора $\overrightarrow{dS}$. Для замкнутых поверхностей, если это направление не задано, как правило имеется в виду направление из области, ограниченной поверхностью интегрирования, наружу. В зависимости от направления выбирается порядок касательных векторов в произведении.
Задание: Разберите решения задач № 4362 и 4363 из Демидовича, после чего решите следующие номера: