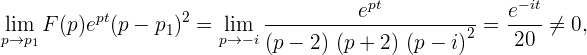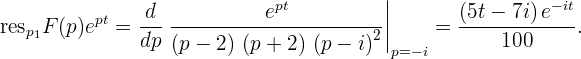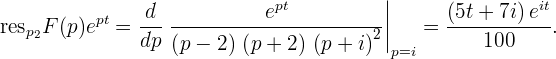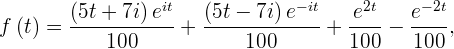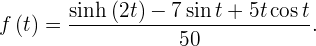Найти оригинал функции:
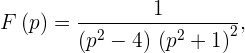 | (1) |
пользуясь второй теоремой разложения.
Согласно второй теореме разложения
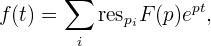 | (2) |
где 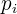 – особые точки функции
– особые точки функции 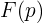 . Найдём особые точки функции (1). Эта функция имеет
полюсы в точках, в которых
. Найдём особые точки функции (1). Эта функция имеет
полюсы в точках, в которых
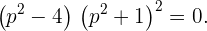
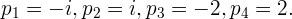
Найдём вычеты 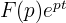 в этих особых точках. Позволю себе напомнить, что
в этих особых точках. Позволю себе напомнить, что 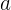 – полюс функции
– полюс функции
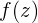 порядка
порядка 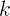 , если
, если
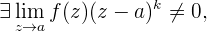
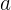 вычисляется по формуле
вычисляется по формуле
![k-1 [ ]||
resaf(z) = ---1----d---- f (z)(z - a )k |
(k - 1 )!dzk -1 |z=a](http://shine.ylsoftware.com/math-img/dk9-33_II/dk9-33_II12x.png)
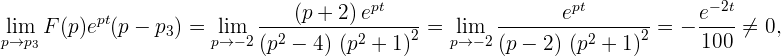
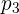 – полюс первого порядка для функции
– полюс первого порядка для функции 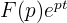 , и
, и
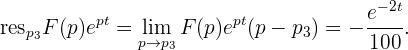
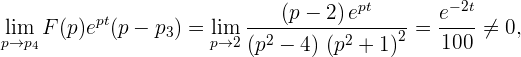
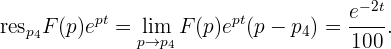
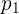 :
: