Ничем особенным решение систем от решения одинарных уравнений не отличается. Но, раз обещал выложить — выкладываю.
Решить систему
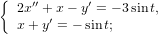
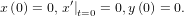
Преобразуем по Лапласу оба уравнения:
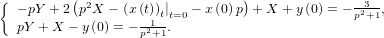
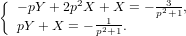
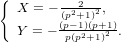
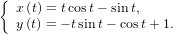
Ничем особенным решение систем от решения одинарных уравнений не отличается. Но, раз обещал выложить — выкладываю.
Решить систему
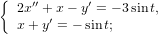
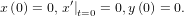
Преобразуем по Лапласу оба уравнения:
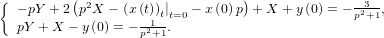
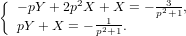
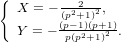
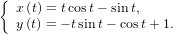
No comments yet.
RSS feed for comments on this post.
Для отправки комментария вам необходимо авторизоваться.
Хостингом угостил Вадим "Moose" Калинников