Циллиндр с радиусом основания
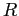
и высотою
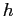
имеет во всё время опыта температуру нижнего основания и боковой поверхности, равную 0
, а температура верхнего основания есть определённая функция от
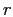
. Найти стационарную температуру внутренних точек циллиндра.
Распределение температуры в непрерывных средах описывается уравнением теплопроводности, которое имеет вид
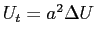
. В стационарной системе температура не меняется со временем (
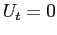
), и уравнение теплопроводности превращается в уравнение Лапласа
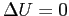
. В циллиндрических координатах оно имеет вид
Учитывая осесимметричность системы, будем считать температуру независимой от координаты
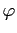
:
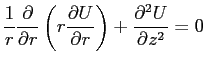 |
(1) |
Будем искать частные решения этого уравнения в виде
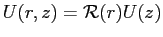
. Тогда
и уравнение в частных производных (
1) распадётся на два обыкновенных дифференциальных уравнения:
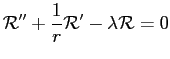 |
(2) |
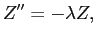 |
(3) |
а граничные условия, допускающие нетривиальные решения, таковы:
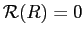
,
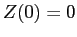
,
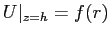
.
Для того, чтобы решить уравнение (
2), заменим
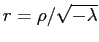
:
Это уравнение есть уравнение Бесселя нулевого порядка с непрерывными решениями вида
При
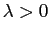
каждое слагаемое этой суммы положительно, решение не имеет нулей и, следовательно, не удовлетворяет граничному условию
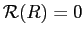
. При
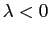
условие
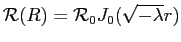
приводит к
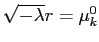
, значит, существует дискретный набор годных значений
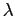
и, соответственно, независимых решений уравнения (
2):
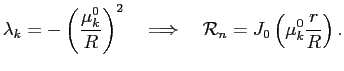 |
(4) |
Теперь рассмотрим уравнение (3). С учётом (4) оно превращается в такое уравнение на отдельные 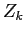 :
:
откуда
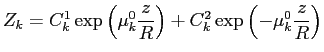
. Учтём граничное условие
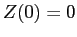
: обозначая
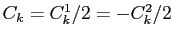
, получим:
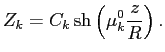 |
(5) |
Общее решение исходного уравнения (1), с учётом (5) и (4), запишется так:
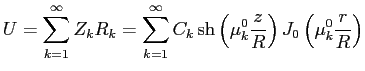 |
(6) |
Коэффициенты
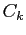
находятся из последнего неучтённого граничного условия:
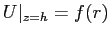
:
Следовательно,
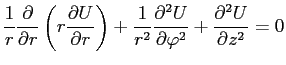
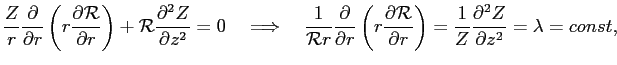
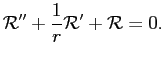
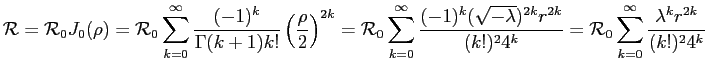
![]() :
:
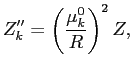
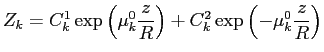 . Учтём граничное условие
. Учтём граничное условие 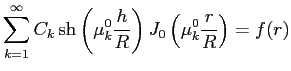
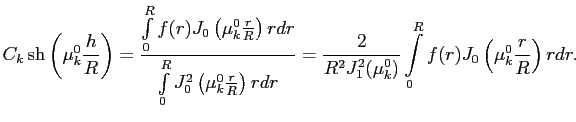
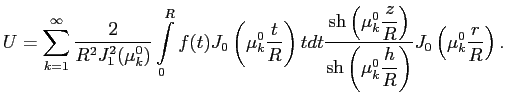
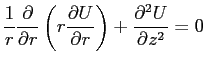
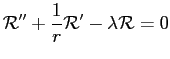
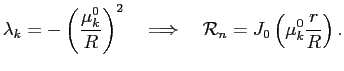
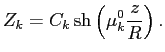
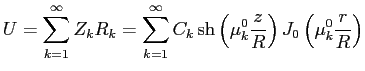

Тимур Юрьевич, если не трудно, разместите пожалуйста решение задачи 132. с полиномами Лежандра.
Комментарий by Маргарита Яковлева — 22.12.2011 @ 10:23 пп
Теперь уже трудно, Маргарита Филипповна. Очень много всего делать надо.
Комментарий by Shine — 23.12.2011 @ 9:18 дп
ну хотя бы нахождение коэффициентов, ибо с ними больше всего возникает проблем. с ответом в методичке никак не сходится мой ответ. по разному пробовала.
Комментарий by Маргарита Яковлева — 23.12.2011 @ 7:14 пп