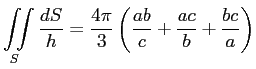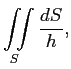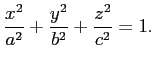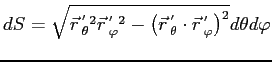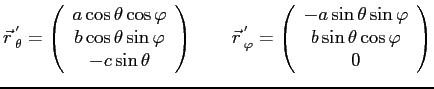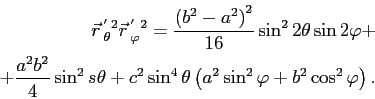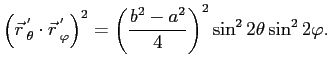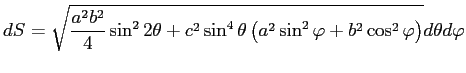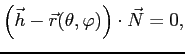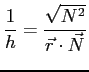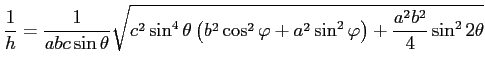Постановка и математическая формулировка задачи
Вычислить интеграл
где ![]() - поверхность эллипсоида, а
- поверхность эллипсоида, а ![]() - расстояние от центра эллипсоида до плоскости, касательной к элементу
- расстояние от центра эллипсоида до плоскости, касательной к элементу ![]() поверхности эллипсоида.
поверхности эллипсоида.
Данный интеграл есть поверхностный интеграл первого рода. Начнём с параметризации поверхности, по которой необходимо провести интегрирование. Так как в задаче выбор системы координат не ограничивается, выберем такую систему координат, чтобы начало координат лежало в центре эллипсоида, а координатные оси совпадали с осями симметрии эллипсоида. Тогда уравнение эллипсоида запишется в каноническом виде:
В обобщённой сферической системе координат, связанной с декартовой системой координат следующими функциями перехода:
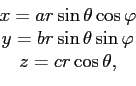
рассматриваемый эллипсоид представляет собой координатную поверхность, и уравнение (2) упростится в ней до следующей формы:
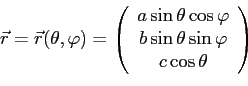
Элемент поверхности 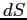
В случае поверхностного интеграла первого рода, каковой мы должны вычислить, скалярный элемент поверхности записывается так:
Производные радиус-вектора
Далее мы опустим промежуточные вычисления в силу громоздкости оных, оставив лишь промежуточные выводы. Квадраты модулей векторов
Скалярное произведение этих векторов приводится к такому виду:
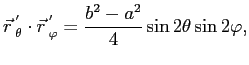
и соответственно,
Подставляя (5) и (6) в (3), получим
Расстояние до касательной плоскости 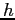
Касательная плоскость к точке
![]() натягивается на касательные векторы
натягивается на касательные векторы
![]() и
и
![]() к этой точке.
Вектор
к этой точке.
Вектор ![]() , как и радиус-вектор любой другой точки, лежащей на касательной плоскости,
удовлетворяет уравнению
, как и радиус-вектор любой другой точки, лежащей на касательной плоскости,
удовлетворяет уравнению
где
С другой стороны вектор
Подставляя
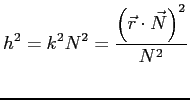
или
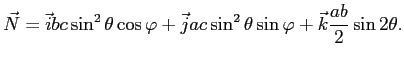 |
(12) |
Отсюда
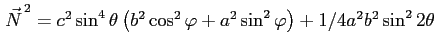 . Подставив эти выражения в (11), получим:
. Подставив эти выражения в (11), получим:
Сопоставив (7) и (13), нетрудно заметить, что
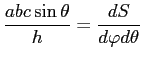
Интегрирование
Подставим в интеграл из (1) выражения для
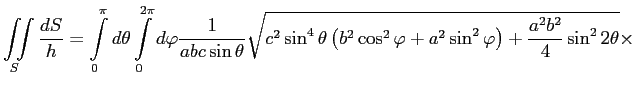
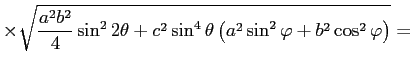 |
(14) |
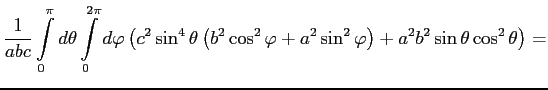
![$\displaystyle \frac{1}{abc}\left[ \int\limits_0^{\pi}d\theta\; c^2\sin^3\theta\...
...arphi+2\pi a^2b^2 \int\limits_0^{\pi}d\theta\;\sin\theta\cos^2\theta \right].
$](http://shine.ylsoftware.com/math-img/dem4347/img43.png)
Взяв входящие в последнее выражение определённые интегралы, получим конечный ответ: