Страница сетевой поддержки учеников Тимура Юрьевича Альпина

Простите меня, в субботу я наговорил ерунды.

При применении второго метода второй дифференциал при наличии связи мы считали так:

1. функцию дифференцировали два раза,
2. В полученный второй дифференциал подставляли приращения некоторых свободных переменных, полученные из уравнения связи.

А он вычисляется сложнее:

1. Функция дифференцируется однажды;
2. В первый дифференциал подставляются приращения (до этого места дело уже сделано при исследовании необходимых условий, т.е. когда искались точки возможного экстремума);
3. Первый дифференциал дифференцируется ещё раз;
4. Опять подставляются приращения.

Этот алгоритм в нормере №3655 (который мы кое-как, каменными топорами, добили) выглядит так.

В задаче требовалось найти экстремумы функции

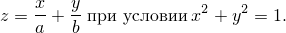
Из условия (оно же уравнение связи) следует, что

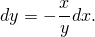(1)

Мы уже нашли, что

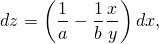
и что стационарных точек (в которых возможен экстремум) в этой задаче две:

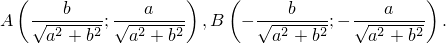
Тогда второй дифференциал будет такой:

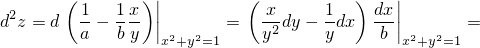
(тут мы подставим (1))

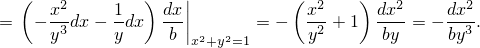
И никаких нулей. Дальнейшее зависит от знака y. Если считать a > 0 и b > 0, то в точке A y = 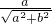> 0, значит - 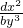< 0 при dx≠0, следовательно, в этой точке достигается максимум. В точке B по аналогичным соображениям достигается минимум.

Третий способ (метод Лагранжа) буду заново рассказывать во вторник. Ко вторнику доделайте номера 3656, 3657.1 и 3659 вторым способом.