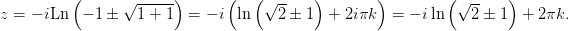Публикуется для гр.620а.
Решить уравнение
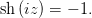
Начнём с того, что ответ, приведённый в методичке, не верен. Если подставить
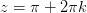в уравнение, получится 0, а не -1. Возможно, это была опечатка в уравнении, но мы будем
действовать по обычному студенческому принципу “что дали - то решаем”.
По определениям
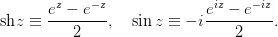
Отсюда можно заметить, что
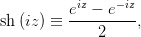
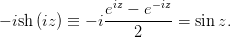
Тогда уравнение можно, домножив обе части на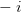 
, привести к виду
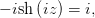
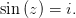 | (1) |
Теперь доделаем то, что вы должны были доделать на позапрошлой паре - решим уравнение
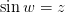вообще и выразим арксинус через логарифм в частности. По определению синуса (см.
выше),
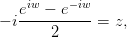
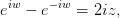
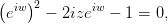
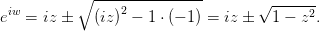
Таким образом,
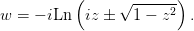 | (2) |
Тут приведено полное решение уравнения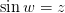
, которое требовалось по условиям задачи. В
виде отступления добавлю, что ветви этой функции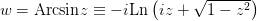 
называются
Арксинусом.
Подставим теперь 
и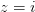 
в 2 и получим решение уравнения 1:
