к гр. 625 « Страница сетевой поддержки учеников Тимура Юрьевича Альпина

Страница сетевой поддержки учеников Тимура Юрьевича Альпина

30.10.2013

к гр. 625

Filed under: пепел — Shine @ 3:09 пп

Сегодня решение уравнения 681 свелось к уравнению
$xy^,_2-y_2=(2x-1)e^{-2x}$ .
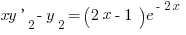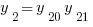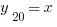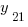Решение искалось в виде $y_2=y_{20}y_{21}$ . Мы быстро нашли, что $y_{20}=x$ , а $y_{21}$ был найден в виде интеграла: $y_{21}=int{}{}{(2/x+1/x^2)e^{-2x} dx}$ .

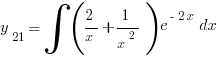Этого интеграла я испугался. Ноутбук тоже. А интеграл, меж тем, легко берётся, если заметить, что:
$d/dx (e^{-2x}/x)=-2 e^{-2x}/x - e^{-2x}/x^2 = -(2/x + 1/x^2)e^{-2x}$ ,
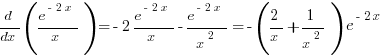и тогда
$int{}{}{(2/x+1/x^2)e^{-2x} dx}=- e^{-2x}/x +C$ .
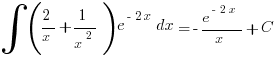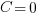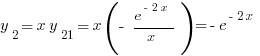При C=0 имеем $y_2=x y_{21}=x (- e^{-2x}/x)=- e^{-2x}$ . Вспомнив, что 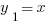$y_{1}=x$ , запишем общее решение уравнения 681:
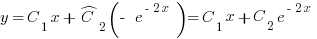$y=C_1 x + hat{C}_2 (- e^{-2x})=C_1 x + C_2 e^{-2x}$ , где $hat{C}_2=-C_2$ ,
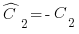что и написано в ответе из задачника.

Возникает вопрос, как можно угадать такую первообразную. Чтобы её не приходилось угадывать, из правой части уравнения можно убрать множитель 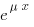$e^{mu x}$ , воспользовавшись методом, изложеным здесь.