Запутали вы меня, тов. Ханафиева и тов. Мубаракшин. Впрочем, я сам хорош, если вам это удалось.
Так вот, cos
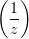 ограничен областью
[−1;1] только для действительного z. Но z может стремиться к нулю не только
по действительной оси. Если z приближается к нулю сверху или снизу, то z = iy,
и тогда
ограничен областью
[−1;1] только для действительного z. Но z может стремиться к нулю не только
по действительной оси. Если z приближается к нулю сверху или снизу, то z = iy,
и тогда
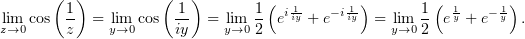
В зависимости от того, снизу или сверху стремится z к нулю, одно из слагаемых в скобке стремится к нулю, а другое к бесконечности, и так быстро, что это не исправит никакое zk. Например, пусть y > 0: t = 1∕y
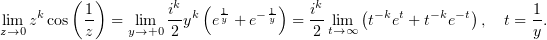
На первом курсе в курсе мат.анализа доказывается, что при ∀k
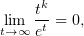
cледовательно предел от обратного выражения бесконечен; в то же время предел
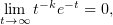
что в совокупности приводит к тому, что
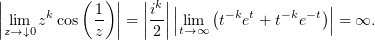
Значит, если умножить cos на любой полином, то z0 = 0 не получится
найти ни предел самой функции (который должен получаться одинаковым при
стремлении к нулю с любой стороны), ни предел, нужный для полюса.
Следовательно эта точка будет существенно особой.
на любой полином, то z0 = 0 не получится
найти ни предел самой функции (который должен получаться одинаковым при
стремлении к нулю с любой стороны), ни предел, нужный для полюса.
Следовательно эта точка будет существенно особой.
