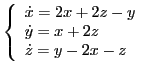 |
(1) |
В матричном виде эта система представляется как
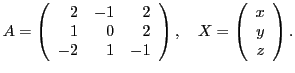 |
(2) |
Собственные значения матрицы
1) Собственный вектор, принадлежащий единице ![]() , ищется из уравнения
, ищется из уравнения
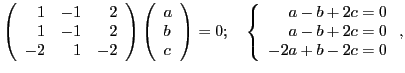 |
(3) |
При
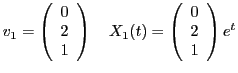 |
(4) |
i) Определяем собственный вектор ![]() :
:
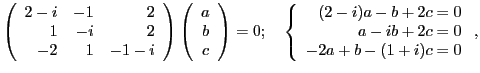 |
(5) |
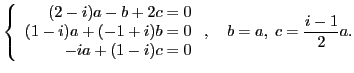 |
(6) |
При
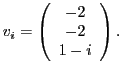 |
(7) |
Составим решение с этим вектором и выделим его действительную и мнимую части:
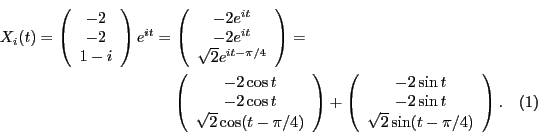
Тогда действительные частные решения системы, соответствующие паре
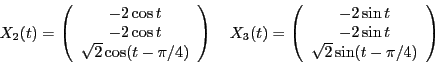
Решение в векторном виде будет записываться в следующем виде:
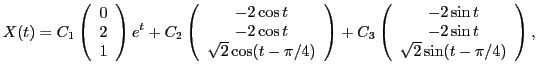 |
(8) |
и после преобразования мы можем предъявить искомые функции:
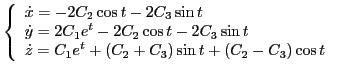 |
(9) |
Я в курсе, что этот ответ не совпадает с данным в задачнике. Однако в ответе можно производить переобозначения констант, совершая в трёхмерном пространстве констант любые невырожденные преобразования, что делает неочевидной (не)тождественность разных решений. С другой стороны, этот ответ подставлялся в исходную систему уравнений, и при помощи системы компьютерной алгебры «Maxima» было получено верное тождество.
