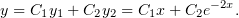Я задал группе 06-410 уравнения, решаемые методом Остроградского-Лиувилля, а примеров не показал. Показываю:
Решить уравнение
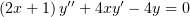 | (1) |
Нам потребуется угадать первое частное решение. Заметим, что если в
уравнение подставить 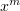 , то во втором и третьем слагаемом
, то во втором и третьем слагаемом  окажется в
равных степенях. Чтобы первое слагаемое уничтожилось, попробуем подставить
в уравнение (1)
окажется в
равных степенях. Чтобы первое слагаемое уничтожилось, попробуем подставить
в уравнение (1)
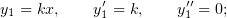
и найти 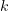 :
:
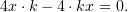
Как видно, последнее выполняется при всяком  ; для простоты мы выберем
частное решение для
; для простоты мы выберем
частное решение для 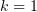 :
:
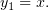
На занятии мы получили, что
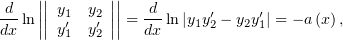
где 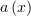 – это коэффициент при
– это коэффициент при 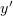 в уравнении, в котором коэффициент при
в уравнении, в котором коэффициент при
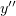 равен единице. Разделив уравнение (1) на
равен единице. Разделив уравнение (1) на 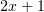 , получим его в нужном
виде:
, получим его в нужном
виде:
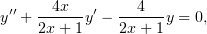
откуда становится видно, что
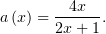
Тогда
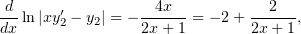
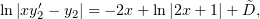
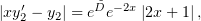
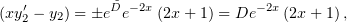 | (2) |
где 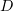 – произвольная константа. Заметим, что
– произвольная константа. Заметим, что
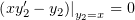
и заменим в уравнении (2)
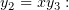
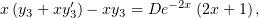
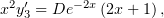
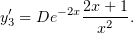
Проинтегрируем:
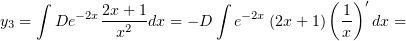
![∫
= − De− 2x 2x-+-1+ D [− 2e−2x(2x+ 1)+ e−2x ⋅2]-1dx =
x x](http://shine.ylsoftware.com/math-img/fil681/fil68127x.png)
![−2x2x+ 1 ∫ [ −2x ] 1
= − De --x---+ D − 4e x x-dx =](http://shine.ylsoftware.com/math-img/fil681/fil68128x.png)
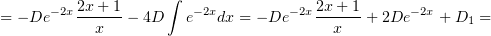
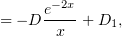
и отсюда найдём
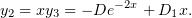
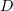 и
и 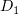 – произвольные константы. Мы ищем частное решение, независимое
от
– произвольные константы. Мы ищем частное решение, независимое
от 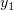 , поэтому мы можем выбрать
, поэтому мы можем выбрать 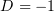 и
и 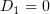 . Тогда
. Тогда
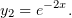
Докажем независимость этих решений:
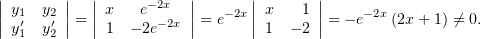
Получив два частных решения, общее запишем как обычно: