Я совершенно неправильно объяснил эту тему. Каюсь, грешен.
Боковая поверхность конуса высоты $h$ и радиуса $r$ получается через
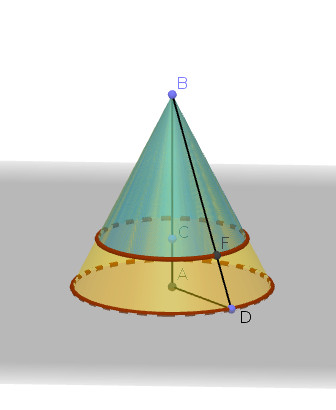
плоскую развёртку в часть круга (рис.1, $AB=h$, $AD=r$, $BD=l$).
|
|
|
рис. 1
|
рис. 2
|
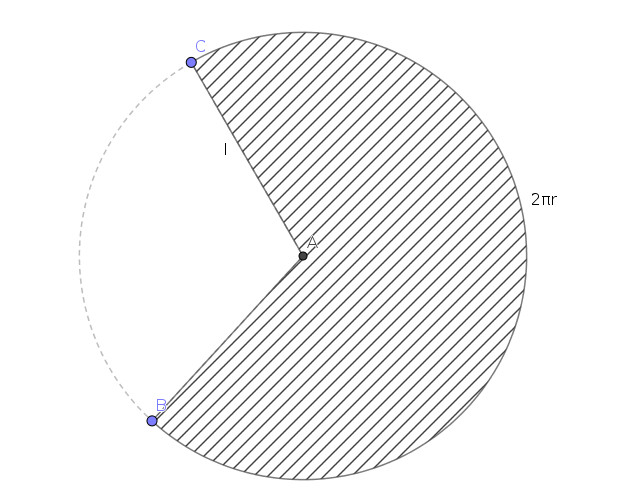
Этот круг имеет радиус, равный $l$ (рис.2); сама боковая поверхность
на нём занимает часть, пропорциональную доле угла развёртки (составляющего
$\frac{2\pi r}{l}$) от полного оборота:
\[
S_{c}=S_{o}k=\pi l^{2}\left(\frac{2\pi r}{l}\frac{1}{2\pi}\right)=\pi lr=\pi\sqrt{r^{2}+h^{2}}r=\pi\sqrt{1+\left(\frac{h}{r}\right)^{2}}r^{2}
\]
Боковая поверхность $\Delta S$ усечённого конуса высоты $\Delta h$
будет равна разности площадей боковых поверхностей конусов, внешнего
и внутреннего (на рис.1 $AB=h_{1}$, $AD=r_{1}$, $BC=h_{2}$, $CF=r_{2}$).
В силу подобия
\[
\frac{h_{1}}{r_{1}}=\frac{h_{2}}{r_{2}}=\frac{h_{2}-h_{1}}{r_{2}-r_{1}}=\frac{\Delta h}{\Delta r}.
\]
Тогда площадь
\[
\Delta S=S_{2}-S_{1}=\pi\sqrt{1+\left(\frac{h_{2}}{r_{2}}\right)^{2}}r_{2}^{2}-\pi\sqrt{1+\left(\frac{h_{1}}{r_{1}}\right)^{2}}r_{1}^{2}=\pi\sqrt{1+\left(\frac{\Delta h}{\Delta r}\right)^{2}}\left(r_{2}^{2}-r_{1}^{2}\right)=\pi\sqrt{1+\left(\frac{\Delta h}{\Delta r}\right)^{2}}\left(r_{2}-r_{1}\right)\left(r_{2}+r_{1}\right).
\]
Боковая поверхность $\Delta S$ усечённого конуса с осью $x$, радиусы
которого задаются функцией $y\left(x\right)$:
\[
r_{1}=y\left(x\right),\quad r_{2}=y\left(x+\Delta x\right),\quad,\Delta r=\Delta y\quad\Delta h=\Delta x
\]
\[
y\left(x\right)>0
\]
\begin{equation}
\Delta S=\pi\sqrt{1+\left(\frac{\Delta x}{\Delta y}\right)^{2}}\Delta y\left[y\left(x\right)+y\left(x+\Delta x\right)\right]=\pi\sqrt{\left(\Delta y\right)^{2}+\left(\Delta x\right)^{2}}\left[y\left(x\right)+y\left(x+\Delta x\right)\right]=\label{eq:bok}
\end{equation}
\[
=\pi\sqrt{\left(\frac{\Delta y}{\Delta x}\right)^{2}+1}\left[y\left(x\right)+y\left(x+\Delta x\right)\right]\Delta x.
\]
Перейдём теперь к нахождению площади тела вращения графика функции
$y\left(x\right)$ вокруг оси $x$. Пусть $x$ лежит от $a$ до $b$.
Разобъём отрезок от $a$ до $b$ на отрезки длиной $\Delta x_{k}=x_{k}-x_{k-1}$,
через концы этих отрезков проведём перпендикулярные к оси $x$ плоскости
и соединим границы сечений коническими поверхностями (рис.3). Полученные
поверхности будут боковыми поверхностями усечённых конусов, чьи площади
$\Delta S_{k}$ будут задаваться формулой (\ref{eq:bok}).
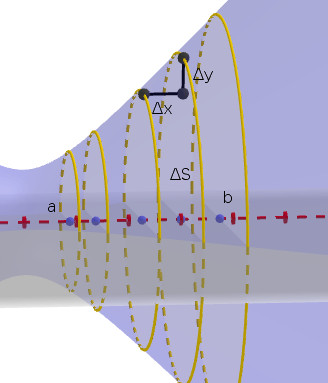
Сумма площадей
$\Delta S_{k}$ образует площадь поверхности, состоящей из участков
конусов и приближающей гладкую поверхность вращения графика функции
$y\left(x\right)$ (подобно тому, как ломаная приближала сам график
при нахождении его длины)
\[
S_{N}=\sum_{k=1}^{N}\Delta S_{k}=\sum_{k=1}^{N}\pi\sqrt{\left(\frac{\Delta y_{k}}{\Delta x_{k}}\right)^{2}+1}\left[y\left(x_{k-1}\right)+y\left(x_{k}\right)\right]\Delta x_{k}.
\]
Предел при $N\to\infty$ и $\max\Delta x_{k}\to0$ этой площади называется
площадью поверхности вращения:
\[
S=\lim_{N\to\infty}S_{N}=\intop_{a}^{b}\frac{dS}{dx}dx,
\]
\[
\frac{dS}{dx}=\lim_{\Delta x\to0}\frac{\Delta S}{\Delta x}=\lim_{\Delta x\to0}\pi\sqrt{\left(\frac{\Delta y}{\Delta x}\right)^{2}+1}\left[y\left(x\right)+y\left(x+\Delta x\right)\right]=2\pi y\sqrt{\left(y'\right)^{2}+1},
\]
\[
S=2\pi\intop_{a}^{b}y\sqrt{\left(y'\right)^{2}+1}dx.
\]
В свете вышесказанного задача №2486 решается так:
\[
y=x\sqrt{\frac{x}{a}}=\frac{x^{3/2}}{\sqrt{a}}
\]
\[
\left(y'\right)^{2}=\left(\frac{3}{2}\frac{x^{1/2}}{\sqrt{a}}\right)^{2}=\frac{9}{4}\frac{x}{a}
\]
\[
S=2\pi\intop_{0}^{a}y\sqrt{\left(y'\right)^{2}+1}dx=2\pi\intop_{0}^{a}\frac{x^{3/2}}{\sqrt{a}}\sqrt{\frac{9}{4}\frac{x}{a}+1}dx
\]
$\sqrt{\frac{x}{a}}=t$, $x^{3/2}=a^{3/2}t^{3}$, $x=at^{2}$, $dx=2atdt$:
\[
S=2\pi\intop_{0}^{a}\frac{x^{3/2}}{\sqrt{a}}\sqrt{\frac{9}{4}\frac{x}{a}+1}dx=2\pi\intop_{0}^{1}\frac{a^{3/2}t^{3}}{\sqrt{a}}\sqrt{\frac{9}{4}\frac{at^{2}}{a}+1}2atdt=4\pi a^{2}\intop_{0}^{1}\sqrt{\frac{9}{4}t^{2}+1}t^{4}dt,
\]
$\frac{3}{2}t=s$ $t=\frac{2}{3}s$ $dt=\frac{2}{3}ds$
\[
S=4\pi a^{2}\intop_{0}^{1}\sqrt{\frac{9}{4}t^{2}+1}t^{4}dt=4\pi a^{2}\intop_{0}^{3/2}\sqrt{s^{2}+1}\left(\frac{2}{3}s\right)^{4}\frac{2}{3}ds=\frac{2^{7}}{3^{5}}\pi a^{2}\intop_{0}^{3/2}\sqrt{s^{2}+1}s^{4}ds=
\]
\[
=\frac{8}{3^{5}}\mathrm{arcsinh}\left(\frac{3}{2}\right)\pi a^{2}+\frac{28\sqrt{13}}{81}\pi a^{2}=\frac{8}{3^{5}}\ln\left|\frac{3}{2}+\sqrt{\left(\frac{3}{2}\right)^{2}+1}\right|\pi a^{2}+\frac{28\sqrt{13}}{81}\pi a^{2}.
\]





