Страница сетевой поддержки учеников Тимура Юрьевича Альпина

Сгоряча я написал единый движок для взятия интегралов №1943, 1944 и 1946. Тут много автоматики и незнакомых команд, за подробностями обращайтесь в мануал максимы.

Задаём полином в числителе

(%i162) P:x^10;

и корень в знаменателе:

(%i163) y:sqrt(1+x^2);

Полюбуемся на полученный интеграл, заодно проверим, всё ли правильно набрали:

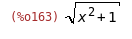
(%i164) int:'integrate(P/y,x);

Назовём буквой n степень числителя:

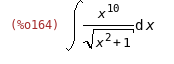
(%i165) n:hipow(P,x);

и создадим полином Q меньшего на единицу порядка:

(%i166) Q:sum(a[n]*x^n,n,0,n-1);

Это формула, стоявшая перед этим блоком номеров в Демидовиче, её надо набрать, чтобы потом использовать. Заметьте, что в неё уже подставились наши обозначения:

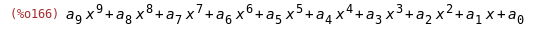
(%i167) fla:'integrate(P/y,x)=Q*y+lambda*'integrate(1/y,x);

Продифференцируем её

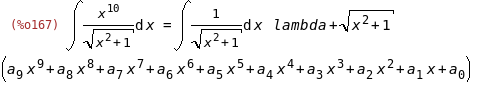
(%i168) diff(%,x);

и умножим полученное на y:

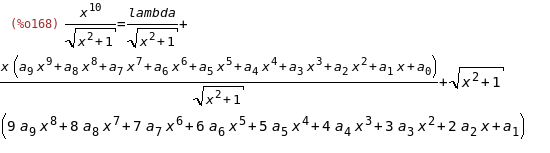
(%i169) expand(%*y);

Приравняем коеффициенты при равных степенях (это таки можно сделать автоматически), составим таким образом систему уравнений:

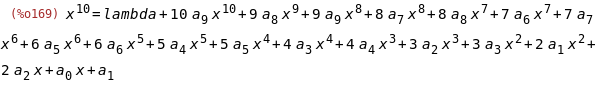
(%i170) sys:makelist(ratcoef(%,x,n-i),i,0,n);

Создадим также список неизвестных коеффициентов,

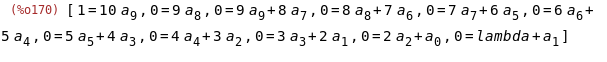
(%i171) makelist(a[i],i,0,n);

Добавим в него лямбду, обозначим,

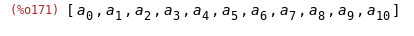
(%i172) var:append(%,[lambda]);

и решим систему, сразу обозначив её решение:

(%i173) coeffs:solve(sys,var)[1];

Подставим теперь коеффициенты в общую формулу,

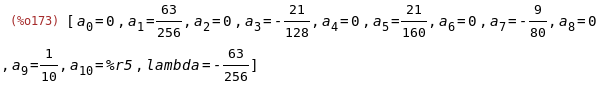
(%i174) fla,coeffs;

и проинтегрируем правую её часть автоматически, чтобы было с чем сравнить ручную работу:

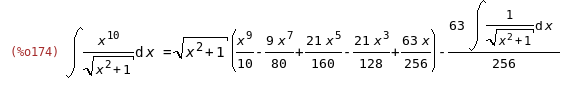
(%i175) rhs(%),integrate;

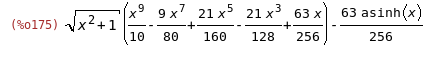
Да, максима не ставит +С в конце. Но вы всё равно должны это делать.