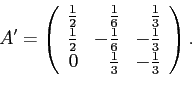Тут я больше показываю, что делать, а кто виноват - в основном оставляю за кадром. Если будут интересны подробности, почему так - пишите, объясню.
Привести к каноническому виду квадратичную форму
и получить матрицу перехода к базису, в котором она будет иметь канонический вид.
Составляем матрицу квадратичной формы (1):
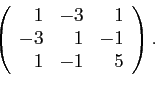
Находим собственные значения этой матрицы (я не буду писать, как это делается, ладно?):
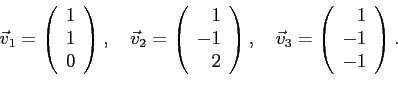
Так как они принадлежат разным собственным значениям, они уже ортогональны и разводить их не надо. Их надо нормировать на единицу, т.е. получить из них новую тройку векторов:
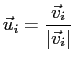
Полученные по этой формуле векторы будут такими:
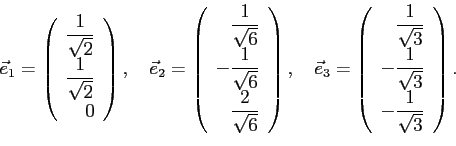
Теперь составляем из координат этих векторов матрицу перехода:
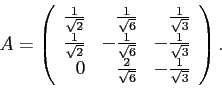
Проверим матрицу
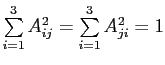 при
при
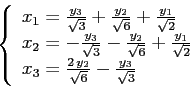
Диагональный вид квадратичной формы будет такой:
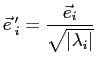 , новые переменные назовём при этом
, новые переменные назовём при этом